Pokud naším cílem je najít relativistické zobecnění Poisson ‚s rovnice pro gravitační pole:
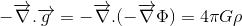
kde Φ označuje gravitační potenciál a ρ k hustota hmoty, jsme na půl cesty.
ve skutečnosti jsme již v našem předchozím článku viděli tenzor energie-hybnosti, že zobecnění hustoty hmoty (pravý termín rovnice) odpovídá Tµv energie-hybnosti.
To se zdá rozumné, pak předpokládat, že naše rovnice by měla mít podobu:
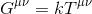
kde k je zkratka pro skalární a Gµv, nazývá Einsteinův tenzor představuje hodnost-2 tenzor popisující zakřivení časoprostoru .
pokud víme, Gµv by se měl řídit následujícími omezeními:
– to by mělo zrušit v plochém prostoročasu
– to by měl popsat zakřivení časoprostoru a být lineární s ohledem na Riemannův tenzor
– to by mělo být symetrické a 2. stupně (jako Tµv)
– to by mělo mít hodnotu null divergence (jako Tµv)
– a konečně, v Newtonovské limity, to by mělo snížit, aby 4nGp
První pokus s Ricciho tenzor jako řešení
připomínáme z našeho článku Geodetické rovnice v Newtonovská limita, že gravitační potenciál Φ je spojena 00-součást metrické prostřednictvím h00=(g00-1)/c2
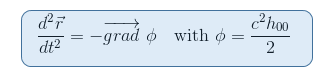
zdá se tedy přirozené hledat tenzor, který zahrnuje druhé derivace metriky, což je případ pro Riemannův tenzor. Dále, Riemannův tenzor je jediným kandidátem, který zatím je schopen popsat zakřivení časoprostoru (viz druhá podmínka výše).
protože musíme najít tenzor rank-2, a pokud předpokládáme, že musíme najít řešení pouze z hlediska Riemannova tenzoru, zdá se přirozené nejprve zvážit smluvní formu Riemannova tenzoru, známého jako Ricciho tenzor.
připomeňme si výraz pro Riemannův tenzor od tha článku Riemannův tenzor křivosti část II: odvození z geodetické deviace
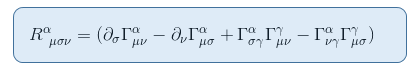
V limitu statické a slabá gravitační pole, pouze jeden termín přispívá k R00:
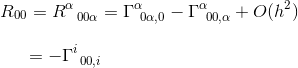
Ve stejném článku, spočítali jsme to Christoffel symbol, a zjistil, že
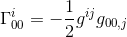
se sbližování právních gij = nij a goo,j = hoo,j (viz článek) jsme si:
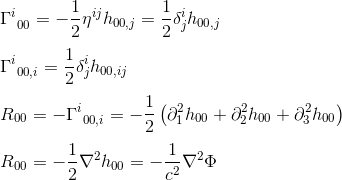
identifikace R00 s ΔΦ (Laplaceova operátora) naznačuje, že pole rovnice obecné teorie relativity by se přirovnat Rab na konstantní násobek Tab.
V roce 1915, pomocí této rovnice, Einstein byl dokonce schopen vyřešit dlouholetý problém Rtuti přísluní precese, což způsobuje psát v listopadu tohoto roku, „Na pár dní, byl jsem bez sebe wih radostné vzrušení.“
nakonec musel Einstein tento první pokus odmítnout, protože obecně se divergence Rab nezruší.
druhý pokus
existuje tenzor úzce související s Ricci skalárním wihchem, který lze umístit na levou stranu bez rozporu. To dává Einsteinův tenzor definovaný následovně:
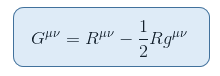
kde R = Raa je Ricciho skalární nebo skalární zakřivení.
tato forma Gab je symetrická a rank-2 a zjevně popisuje zakřivení prostoročasu. Takže zbývá jen ukázat, že totální derivace je nula.
tohle dělat, začneme s Bianchiho identity
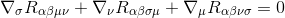
Vynásobením přes gγσgαμgβν (metriky deriváty jsou nulové, takže se chovají jako konstanty a může být přijata uvnitř deriváty), to se poddá:
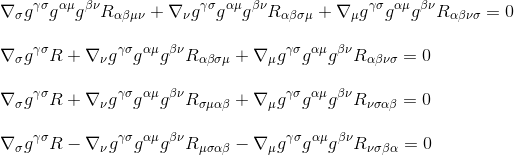
pomocí Ricciho tenzor definice Rµv=gμβgνσRβσ (krok 3) a o přejmenování indexů (krok 4), dostaneme
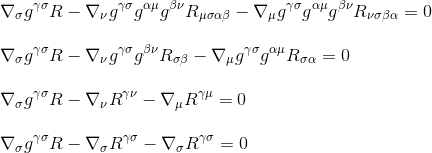
Tím, factorising derivace, jsme se konečně získat
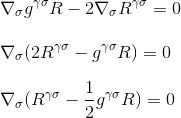
což je přesně to, co jsme chtěli prokázat: divergence Einsteinův tenzor je null, a my jsme našli vhodného kandidáta na levé straně naší zakřivení/hmota-energie rovnice.