Overland flow (nebo povrchový odtok) se vyskytuje ve dvou případech:
1. když intenzita srážek, která dosáhne povrchu, překročí infiltrační kapacitu půdy. Tento proces je známý jako hortonian overland flow.
2. když kombinace intenzity a trvání srážek (a náběhu z vyšších oblastí) nasycuje půdu a zvyšuje hladinu vody na povrch. Tento proces je známý jako saturace po souši.
případové studie: Nizozemsko; Belgie; Španělsko; Keňa; Ghana, Keňa a Mali
Viz také:
- Dřezy
- Hortonian a sytost overland flow (Infiltrace)
Technické Informace
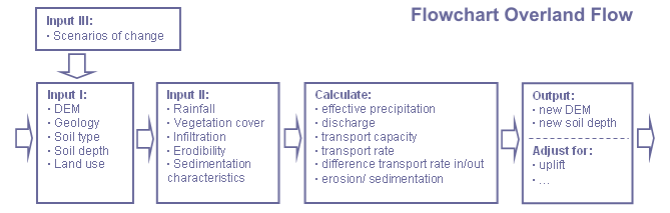
vodní eroze a sedimentace modul model má dva základní předpoklady: 1) potenciální energie povrchových vod toku je hnací silou pro transport sedimentů a 2) rozdíl mezi sedimentu vstup a výstup z buňky mřížky se rovná čisté zvýšení skladování (rovnice kontinuity pro pohyb sediment) (Schoorlova et al., 2000). Popis postupu je odvozen od raných děl z Kirkby (Kirkby, 1971) a Podporovat a Meyer (Foster a Meyer, 1972a; Foster a Meyer, 1972b), kteří používají 2D vzorce pro výpočet vodní eroze a sedimentace. Pro model LAPSUS jsou vzorce přizpůsobeny tak, aby byly schopny simulovat prostorovou (3D) vodní erozi a sedimentaci (Schoorl et al., 2000). Vzorců je uvedeno níže, jsou založeny na 2D vzorce Kirkby a Podporovat a Meyer a doprovodných jednotek (Foster a Meyer, 1972a; Foster a Meyer, 1972b; Kirkby, 1971).
Po výpočtu výtok Q sedimentu přepravní kapacita C (m2 času-1) v mřížce buněk lze vypočítat jako funkci vybíjení a po svahu:
(1.1) C = α·Qm·Λn
Přičemž Λ je svažitost (∂z/∂x) (-) a m (-) a n (-) jsou konstanty, které dává představu o systému studoval: m = 0 a n = 1 naznačuje půdy tečení, při m = n = 3 naznačuje velkých řek (Kirkby, 1971). Nelze dát žádné přísné hranice, protože účinek m A n závisí na interakcích s jinými parametry modelu. Fiktivní proměnná α se používá k opravě jednotek.
rychlost transportu sedimentu S (m2 time-1)se vypočítá podle integrované rovnice kontinuity pro pohyb sedimentu (Eq. 1.2 a 1.3). Složení e-power výraz ve vzorci závisí na rovnováze mezi mírou dopravní sedimentu již v dopravě S0 (m2 času-1) (příchozí sedimentu tavidla pro všechny vyšší sousedy v mřížce buněk) a sediment přepravní kapacita C: pokud S0 < C erozi výsledky, zatímco při S0 > C sedimentace výsledky. Když je buňka mřížky erodována, použije se následující vzorec pro rychlost transportu sedimentů S:
(1.2) S = C + (S0 – C)·e -dx·D/C
Když sedimenty jsou uloženy v mřížce buňky následující vzorec pro transport sedimentů rychlost S se používá:
(1.3) Y = C + (S0 – C)·e -dx·T/C
Přičemž přepravní rychlost sedimentu S více než velikost buňky mřížky dx (m) je vypočítána porovnáním sedimentu přepravní kapacitu C s přepravní rychlost sedimentu již v dopravě S0 (m2 času-1) minus sedimentu přepravní kapacitu C, snížené o e-moc vyplývající z velikost buňky mřížky, kapacita oddělení D nebo vypořádání kapacita T a sedimentu přepravní kapacita C.
Oddělení kapacita D (m čas-1), což představuje jak snadné sedimentu je erodované povrchu, je vypočtena jako funkce vypouštění a sklon podle:
(1.4) D = Kes·Q·Λ
přičemž Kes (m-1) je koncentrovaný povrchový faktor označující erodibility povrchu. Vypořádání kapacita T (m čas-1), což představuje jak snadné sedimentu je uložen na povrchu, se vypočítá následující:
(1.5) D = Pes·Q·Λ
kdy Vsz (m-1) je faktor povrchu označující soustředěné sedimentační vlastnosti.
porovnáním sediment dopravní frekvence je z mřížky buněk s sedimentu již v dopravě S0 změny v transportu splavenin sazba dS, a tedy eroze nebo sedimentace, lze vypočítat následující:
(1.6) dS = S – S0
dS může být přepočítána k eroze nebo sedimentace v metru vydělením mřížky délky dx (m) a násobením časový krok (čas). Výsledná hodnota se používá k opravě digitálního modelu nadmořské výšky a mapy hloubky půdy pro následující časový krok.
srovnání e-síla určuje, jak moc rozdílu mezi přepravní kapacity C a dopravní rychlost sedimentu S může být „spokojený“ v mřížce buněk. V závislosti na hodnotách příslušných proměnných se výsledný výkon e pohybuje mezi 0 a 1. V extrémních situacích, kdy jsou kombinace dx a D/T mnohem větší než C, se e-výkon blíží nule a transportní rychlost sedimentu S se rovná přepravní kapacitě sedimentu C. pak je dosaženo maximální eroze nebo sedimentace. Nicméně, v druhý extrém, kdy dx a D/T dohromady jsou mnohem menší než C, e-power přístupy 1 a dopravní rychlost sedimenty S je rovna přepravní rychlost sedimentů již v dopravě S0 a bez eroze nebo depozice dochází. V méně extrémních situacích modelu je simulovat transport sedimentů rychlost S blízko přepravní kapacita C. V případě S0 > C více sedimentu je transportován, než by bylo povoleno na základě mřížky buněk vyšší a nižší než maximální sedimentu je uložen. E-power proto výsledky v pod-koncentrované a super-koncentrované toky v modelu, vyhlazování eroze a depozice nad svahem. Je zřejmé, že výsledek srovnání e-power je velmi vlivný pro erozi a sedimentaci. Porovnání Eq. 1.1 a 1.4/1.5 je jasné, že výtok a sklon jsou zapojené v obou přepravní kapacity C a při výpočtech oddělení kapacita D nebo vypořádání kapacita T. To znamená, že v situaci, kdy m = n = 1, termín v. e-power snižuje dx ·Kes nebo dx ·Pes. Jako velikost buňky mřížky je konstantní hodnota, erodibility Kes a sedimentability Pes jsou nejdůležitější proměnné v situaci s nízkými hodnoty m a n. Když jsou m A n větší, zvyšuje se účinek přepravní kapacity C na termín e-power. Výsledek termínu e-power je v této situaci těžší předvídat.