Overland flow (tai pintavalunta) esiintyy kahdessa tapauksessa:
1. kun pintaan saapuvan Sademäärän voimakkuus ylittää maaperän tunkeutumiskyvyn. Tämä prosessi tunnetaan nimellä Hortonian overland flow.
2. kun sateen voimakkuus ja kesto (ja ylemmiltä alueilta tuleva valuminen) yhdessä kyllästävät maaperän ja nostavat pohjaveden pintaan. Tämä prosessi tunnetaan saturation overland flow.
tapaustutkimukset: Alankomaat; Belgia; Espanja; Kenia; Ghana, Kenia ja Mali
Katso myös:
- uppouma
- Hortonian ja saturaatioylivirtaus (tunkeutuminen)
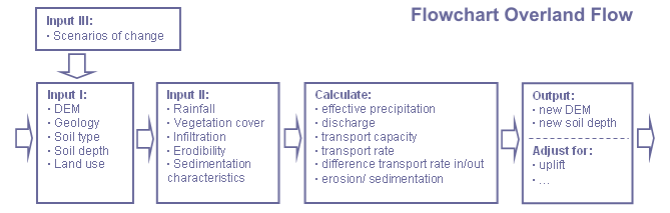
TEKNISET TIEDOT
mallin Vesieroosio-ja sedimentaatiomoduulilla on kaksi perusoletusta: 1) pintaveden virtauksen potentiaalienergia on sedimentin kuljetuksen käyttövoima ja 2) ruudukon sedimentin syötön ja tuotoksen välinen ero on yhtä suuri kuin varastoinnin nettolisäys (sedimentin liikkeen jatkuvuusyhtälö) (Schoorl et al., 2000). Prosessikuvaus on peräisin kirkbyn (Kirkby, 1971) ja Foster and Meyerin (Foster and Meyer, 1972a; Foster and Meyer, 1972b) varhaisista teoksista, joissa veden eroosiota ja sedimentaatiota lasketaan 2D-kaavoilla. LAPSUS-mallin kaavat on mukautettu simuloimaan spatiaalista (3D) veden eroosiota ja sedimentaatiota (Schoorl et al., 2000). Alla käsitellyt kaavat perustuvat Kirkbyn ja Fosterin ja Meyerin 2D-kaavoihin sekä niihin liittyviin yksiköihin (Foster and Meyer, 1972a; Foster and Meyer, 1972b; Kirkby, 1971).
purkauksen Q laskemisen jälkeen sedimentin kuljetuskapasiteetti C (M2 aika-1) ruudukossa voidaan laskea purkauksen ja kaltevuuden funktiona seuraavan:
(1.1) C = α·Qm * Λn
jolloin Λ on kaltevuusgradientti (∂z/∂x) (-) ja m (-) ja n (-) ovat vakioita, jotka antavat viitteitä tutkitusta järjestelmästä: m = 0 ja n = 1 viittaavat maaperän ryömintään, kun taas m = N = 3 viittaa suuriin jokiin (Kirkby, 1971). Tiukkoja rajoja ei voida antaa, sillä m: n ja n: n vaikutus riippuu vuorovaikutuksesta muiden malliparametrien kanssa. Valemuuttujaa α käytetään yksiköiden korjaamiseen.
sedimentin siirtymisnopeus S (m2-aika-1) lasketaan sedimentin liikkeen integroidun jatkuvuusyhtälön (Eq. 1, 2 ja 1, 3). Kaavassa käytetyn E-tehotermin koostumus riippuu jo kuljetuksessa S0 olevan sedimentin siirtymisnopeuden (m2-aika-1) ja sedimentin kuljetuskapasiteetin C välisestä tasapainosta: jos S0 < C eroosiota, kun taas S0 > C sedimentaatiota. Kun hilasolu rapautuu, käytetään seuraavaa kaavaa sedimentin siirtymisnopeudelle S:
(1.2) S = C + (S0 – C)·E-dx * D / C
kun sedimentit kerrostuvat ruudukkoon, käytetään seuraavaa kaavaa sedimentin siirtymisnopeudelle S:
(1.3) S = C + (S0 – C)·E-dx·T/C
jossa sedimentin s siirtonopeus hilasolukoon DX (m) nähden lasketaan vertaamalla sedimentin kuljetuskapasiteettia C jo kuljetuskapasiteettiin S0 (m2 aika-1) vähennettynä sedimentin kuljetuskapasiteetilla C vähennettynä e-teholla, joka johtuu ruudukon koosta, irtautumiskapasiteetista D tai settoutumiskapasiteetista T ja sedimentin kuljetuskapasiteetista C.
Irtoamiskapasiteetti D (M aika-1), joka kuvaa sitä, kuinka helposti sedimentti kuluttuu pinnasta, lasketaan purkautumisen ja kaltevuuden funktiona seuraavan:
(1.4) D = Kes * Q * Λ
, jolloin Kes (m-1) on möykkyinen pintakerroin, joka ilmaisee pinnan erodibiliteettia. Settlement capacity T (m time-1), joka kuvaa kuinka helppoa sedimentti on talletettu pinnalle, lasketaan seuraavasti::
(1.5) D = Pes·Q·Λ
, jolloin Pes (m-1) on pinnoitekerroin, joka ilmaisee kyhmyisiä sedimentaatio-ominaisuuksia.
vertaamalla ruutusolun sedimentin siirtonopeutta S jo kuljetuksessa S0 sedimentin siirtonopeuden DS muutos ja siten eroosio tai sedimentaatio voidaan laskea seuraavasti:
(1.6) dS = s-S0
DS voidaan laskea uudelleen eroosiolle tai sedimentaatiolle metreinä jakamalla se hilapituudella dx (m) ja kertomalla se aika-askeleella (time). Saatua arvoa käytetään korjaamaan digitaalista korkeusmallia ja maan syvyyskarttaa seuraavaa aikavaihetta varten.
e-tehon vertailu määrittää, kuinka suuri osa siirtokapasiteetin C ja sedimentin s siirtonopeuden erosta voidaan ”tyydyttää” ruutukennossa. Riippuen kyseessä olevien muuttujien arvoista, e-potenssin tulos vaihtelee välillä 0 ja 1. Ääritilanteissa, joissa dx ja D/T yhdessä ovat paljon suuria kuin C, E-teho lähestyy nollaa ja sedimentin s kuljetusnopeus on yhtä suuri kuin sedimentin kuljetuskapasiteetti C. silloin saavutetaan suurin eroosio tai sedimentaatio. Kuitenkin toisessa ääripäässä, kun dx ja D/T yhdessä ovat paljon pienempiä kuin C, E-teho lähestyy 1 ja sedimenttien siirtonopeus S on yhtä suuri kuin jo kuljetuksessa S0 olevien sedimenttien siirtonopeus eikä eroosiota tai laskeumaa tapahdu. Lievemmissä äärimmäisissä tilanteissa malli todennäköisesti simuloi sedimentin siirtonopeutta S lähellä kuljetuskapasiteettia C. tapauksessa S0 > C sedimenttiä kuljetetaan enemmän kuin olisi sallittua yläpuolella olevien ruudukon solujen perusteella ja vähemmän kuin maksimisedimentti kerrostuu. E-power johtaa siis mallissa alikonsentroituneisiin ja superkonsentroituneisiin virtauksiin tasoittaen eroosiota ja laskeumaa Rinteen yli. E-power-vertailun tulos vaikuttaa selvästi eroosioon ja sedimentaatioon. Vertaamalla Eq. 1.1 ja 1.4 / 1.5 on selvää, että purkaus ja kaltevuus liittyvät sekä kuljetuskapasiteettiin C että irrotuskapasiteetin D tai siirtokapasiteetin t laskelmiin.tämä tarkoittaa sitä, että tilanteessa, jossa m = n = 1, termi e-potenssissa pienenee muotoon dx ·Kes tai DX ·Pes. Koska hilasolun koko on vakioarvo, erodibility Kes ja sedimentability Pes ovat tärkeimmät muuttujat tilanteessa, jossa M-ja n-arvot ovat alhaiset. Kun m ja n ovat suurempia, siirtokapasiteetin C vaikutus e-potenssitermiin kasvaa. E-power-termin lopputulosta on siinä tilanteessa vaikeampi ennustaa.