Logaritmi: Introducere în „relația”

reveniți la indexul lecțiilor / faceți lecțiile în ordine / pagina prietenoasă cu tipărirea

logaritmi: Introducere în
„relația” (pagina 1 din 3)

secțiuni: Introducere în jurnale, simplificarea expresiilor jurnalelor, jurnalele comune și naturale

logaritmii sunt „opusul” exponențialelor, la fel cum scăderea este opusul adunării și împărțirea este opusul înmulțirii. Jurnalele” anulează ” exponențialele. Din punct de vedere tehnic, jurnalele sunt inversele exponențialelor.

în termeni practici, mi s-a părut util să mă gândesc la jurnale în ceea ce privește relația:

în partea stângă de mai sus este declarația exponențială „y = bx”. În partea dreaptă de mai sus, „logb(y) = x” este declarația logaritmică echivalentă, care se pronunță „log-base-B de y este egal cu x”; valoarea abonatului „b” este „baza logaritmului”, la fel cum b este baza în expresia exponențială „bx”. Și, la fel cum baza b dintr-un exponențial este întotdeauna pozitivă și nu egală cu 1, la fel și baza b pentru un logaritm este întotdeauna pozitivă și nu egală cu 1. Orice se află în interiorul logaritmului se numește „argumentul” jurnalului. Rețineți că baza atât în ecuația exponențială, cât și în ecuația jurnal (de mai sus) este „b”, dar că X și y schimbă laturile atunci când comutați între cele două ecuații.

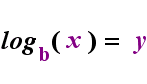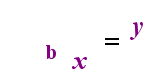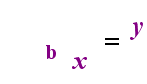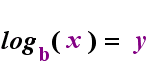
dacă vă puteți aminti această relație (că oricare ar fi fost argumentul jurnalului devine „egal” și orice ar fi fost „egal” devine exponentul în exponențial și invers), atunci nu ar trebui să aveți prea multe probleme cu logaritmii.

(eu însumi am inventat termenul „relația”. Nu o veți găsi în textul dvs., iar profesorii și tutorii dvs. nu vor avea nicio idee despre ce vorbiți dacă le menționați. „Relația” este o terminologie complet non-standard. De ce o folosesc oricum? Pentru că funcționează.)

apropo: dacă ați observat că am schimbat variabilele între cele două casete care afișează „relația”, aveți un ochi ascuțit. Am făcut asta intenționat, pentru a sublinia că ideea nu este variabilele în sine, ci modul în care se mișcă.

• convertiți „63 = 216” la expresia logaritmică echivalentă.

pentru a converti, baza (adică 6)rămâne aceeași, dar 3 și 216 schimbă laturile. Acest lucru îmi dă:

log6(216) = 3 drepturi de autor Elizabeth Stapel 2002-2011 Toate drepturile rezervate

• convertiți „log4 (1024) = 5” la expresia exponențială echivalentă.

pentru a converti, baza (adică 4) rămâne aceeași, dar 1024 și 5 schimbă laturile. Acest lucru îmi dă:

45 = 1024

Top| 1 | 2 | 3 | Înapoi la Index următor >>