vă rugăm să furnizați Numere separate prin virgulă pentru a calcula.
Calculator de statistici înrudite / Calculator de deviație Standard / Calculator de dimensiune a eșantionului
înseamnă
cuvântul înseamnă, care este un omonim pentru mai multe alte cuvinte în limba engleză, este la fel de ambiguu chiar și în domeniul matematicii. În funcție de context, indiferent dacă este matematic sau statistic, ceea ce se înțelege prin „medie” se schimbă. În cea mai simplă definiție matematică privind seturile de date, media utilizată este media aritmetică, denumită și așteptare matematică, sau medie. În această formă, media se referă la o valoare intermediară între un set discret de numere, și anume, suma tuturor valorilor din setul de date, împărțită la numărul total de valori. Ecuația pentru calcularea unei medii aritmetice este practic identică cu cea pentru calcularea conceptelor statistice de populație și medie a eșantionului, cu ușoare variații ale variabilelor utilizate:
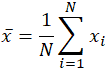
media este adesea notată ca x, pronunțată „X bar” și chiar și în alte utilizări atunci când variabila nu este x, notația cu bare este un indicator comun al unei forme de medie. În cazul specific al populației înseamnă, mai degrabă decât folosind variabila x,se folosește simbolul grecesc MU, sau Ecuator. În mod similar, sau mai degrabă confuz, media eșantionului din statistici este adesea indicată cu un capital X. Având în vedere setul de date 10, 2, 38, 23, 38, 23, 21, aplicarea sumării de mai sus randamente:
|
10 + 2 + 38 + 23 + 38 + 23 + 21
|
= | = 22.143 |
după cum sa menționat anterior, aceasta este una dintre cele mai simple definiții ale mediei, iar altele includ media aritmetică ponderată (care diferă doar prin faptul că anumite valori din setul de date contribuie cu mai multă valoare decât altele) și media geometrică. Înțelegerea corectă a situațiilor și contextelor date poate oferi adesea unei persoane instrumentele necesare pentru a determina ce metodă relevantă statistic să folosească. În general, media, mediana, modul și intervalul ar trebui, în mod ideal, să fie calculate și analizate pentru un anumit eșantion sau set de date, deoarece ele elucidează diferite aspecte ale datelor Date și, dacă sunt luate în considerare singure, pot duce la denaturări ale datelor, așa cum se va demonstra în secțiunile următoare.
mediană
conceptul statistic al medianei este o valoare care împarte un eșantion de date, o populație sau o distribuție de probabilitate în două jumătăți. Găsirea medianei implică în esență găsirea valorii într-un eșantion de date care are o locație fizică între restul numerelor. Rețineți că atunci când se calculează mediana unei liste finite de numere, ordinea eșantioanelor de date este importantă. În mod convențional, valorile sunt listate în ordine crescătoare, dar nu există niciun motiv real pentru care listarea valorilor în ordine descrescătoare ar oferi rezultate diferite. În cazul în care numărul total de valori dintr-un eșantion de date este impar, mediana este pur și simplu numărul din mijlocul listei tuturor valorilor. Când eșantionul de date conține un număr par de valori, mediana este media celor două valori medii. Deși acest lucru poate fi confuz, amintiți-vă pur și simplu că, deși mediana implică uneori calculul unei medii, atunci când apare acest caz, va implica doar cele două valori medii, în timp ce o medie implică toate valorile din eșantionul de date. În cazurile impare în care există doar două eșantioane de date sau există un număr par de eșantioane în care toate valorile sunt aceleași, media și mediana vor fi aceleași. Având în vedere același set de date ca înainte, mediana ar fi obținută în felul următor:
2,10,21,23,23,38,38
după listarea datelor în ordine crescătoare și determinarea faptului că există un număr impar de valori, este clar că 23 este mediana dată acestui caz. Dacă ar exista o altă valoare adăugată la setul de date:
2,10,21,23,23,38,38,1027892
deoarece există un număr par de valori, mediana va fi media celor două numere medii, în acest caz 23 și 23, a căror medie este 23. Rețineți că în acest set de date special, adăugarea unui outlier (o valoare cu mult în afara intervalului de valori așteptat), valoarea 1.027.892, nu are niciun efect real asupra setului de date. Dacă totuși media este calculată pentru acest set de date, rezultatul este 128,505.875. Această valoare nu este în mod clar o bună reprezentare a celorlalte șapte valori din setul de date care sunt mult mai mici și mai apropiate ca valoare decât media și outlier. Acesta este principalul avantaj al utilizării medianei în descrierea datelor statistice în comparație cu media. În timp ce ambele, precum și alte valori statistice, ar trebui calculate la descrierea datelor, dacă se poate utiliza doar una, mediana poate oferi o estimare mai bună a unei valori tipice într-un set de date dat atunci când există variații extrem de mari între valori.
mod
în Statistici, Modul este valoarea dintr-un set de date care are cel mai mare număr de recurențe. Este posibil ca un set de date să fie multimodal, ceea ce înseamnă că are mai multe moduri. De exemplu:
2,10,21,23,23,38,38
atât 23, cât și 38 apar de două ori fiecare, făcându-le ambele un mod pentru setul de date de mai sus.
similar cu media și mediana, modul este folosit ca o modalitate de a exprima informații despre variabile și populații aleatorii. Spre deosebire de medie și mediană cu toate acestea, modul este un concept care poate fi aplicat la valori non-numerice, cum ar fi marca de tortilla chips-uri cel mai frecvent achiziționate de la un magazin alimentar. De exemplu, atunci când se compară mărcile Tostitos, Mission și XOCHiTL, dacă se constată că în vânzarea chipsurilor tortilla, XOCHiTL este modul și se vinde într-un raport 3:2:1 comparativ cu Tostitos și, respectiv, chipsurile tortilla marca Mission, raportul ar putea fi utilizat pentru a determina câte pungi din fiecare marcă să stocheze. În cazul în care 24 de pungi de chipsuri tortilla se vând într-o anumită perioadă, magazinul ar stoca 12 pungi de Jetoane XOCHiTL, 8 de Tostitos și 4 de misiune dacă se utilizează modul. Dacă totuși magazinul a folosit pur și simplu o medie și a vândut 8 pungi din fiecare, ar putea pierde 4 vânzări dacă un client dorește doar jetoane XOCHiTL și nu orice altă marcă. După cum reiese din acest exemplu, este important să se ia în considerare toate manierele valorilor statistice atunci când se încearcă să se tragă concluzii cu privire la orice eșantion de date.
interval
intervalul unui set de date din statistici este diferența dintre cele mai mari și cele mai mici valori. În timp ce gama are semnificații diferite în diferite domenii ale statisticilor și matematicii, aceasta este definiția sa cea mai de bază și este ceea ce este folosit de calculatorul furnizat. Folosind același exemplu:
2,10,21,23,23,38,38
38 – 2 = 36
intervalul din acest exemplu este 36. În mod similar cu media, intervalul poate fi afectat semnificativ de valori extrem de mari sau mici. Folosind același exemplu ca anterior: