dacă scopul nostru este de a găsi generalizarea relativistă a ecuației lui Poisson pentru câmpul gravitațional:
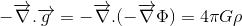
unde se referă la potențialul gravitațional și la densitatea de masă, Suntem la jumătatea drumului.
într-adevăr, am văzut deja în articolul nostru anterior tensorul energie-impuls că generalizarea densității de masă (termenul din dreapta al ecuației) corespunde impulsului energetic t XVV.
pare rezonabil atunci să presupunem că ecuația noastră ar trebui să ia forma:
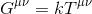
unde k reprezintă un scalar și G, numit tensorul Einstein reprezintă un tensor de rang – 2 care descrie curbura spațiu-timp .
din câte știm, g-v ar trebui să respecte următoarele constrângeri:
– ar trebui să anuleze în spațiu – timp plat
– ar trebui să descrie curbura spațiu – timp și să fie liniară în ceea ce privește tensorul Riemann
– ar trebui să fie simetrică și de rangul 2 (ca T Olfvv)
-ar trebui să aibă o divergență nulă (ca T Olfvv)
-ar trebui să se reducă la 4ngp
prima încercare cu tensorul Ricci ca soluție
ne amintim din articolul nostru ecuația geodezică în limita newtoniană că potențialul gravitațional Irakul este legat de componenta 00 a metricii prin H00=(G00-1)/C2
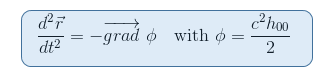
atunci pare firesc să căutăm un tensor care implică al doilea derivat al metricii, ceea ce este cazul tensorului Riemann. Mai mult, tensorul Riemann este singurul candidat pe care îl cunoaștem până acum pentru a putea descrie curbura spațiu-timp (cf a doua constrângere de mai sus).
deoarece trebuie să găsim un tensor de rang-2 și dacă presupunem că trebuie să găsim o soluție numai în ceea ce privește tensorul Riemann, pare firesc să luăm în considerare mai întâi forma contractată a tensorului Riemann, cunoscut sub numele de tensorul Ricci.
pentru a vedea acest lucru, să ne amintim expresia tensorului Riemann din articolul tensorul de curbură Riemann partea II: derivarea din deviația geodezică
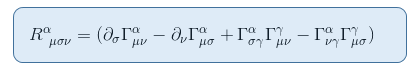
în limita unui câmp gravitațional static și slab, un singur termen contribuie la R00:
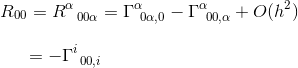
în același articol, am calculat acest simbol Christoffel și am constatat că
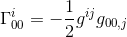
cu aproximarea gij = INJ și goo, j = hoo, j (consultați articolul) obținem:
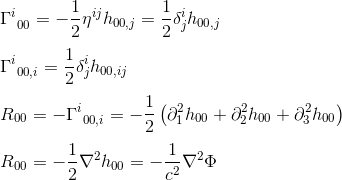
identificarea lui R00 cu ecuația de câmp (Operator Laplacian) sugerează că ecuația câmpului în relativitatea generală ar trebui să echivaleze Rab cu un multiplu constant de tab.
în 1915, folosind această ecuație, Einstein a fost chiar capabil să rezolve problema de lungă durată a precesiei periheliului Mercur, determinând să scrie în noiembrie acel an că, „pentru câteva zile, am fost alături de mine cu emoție veselă.”
în cele din urmă, Einstein a trebuit să respingă această primă încercare, datorită faptului că, în general, divergența Rab nu anulează.
a doua încercare
există tensor strâns legat de scalarul Ricci wihch poate fi pus pe partea stângă fără contradicție. Aceasta dă tensorul Einstein definit după cum urmează:
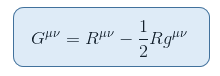
unde R = Raa este scalarul Ricci sau curbura scalară.
această formă de Gab este simetrică și de rang-2 și descrie în mod evident curbura spațiu-timp. Deci, rămâne doar să arătăm că derivata totală este zero
pentru a face acest lucru, începem cu identitatea Bianchi
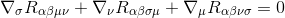
înmulțindu-se cu g-x-x-x-x-x-x-x (derivatele metrice sunt zero, deci acționează ca constante și pot fi luate în interiorul derivatelor), rezultă la:
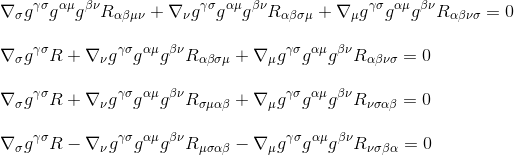
prin utilizarea definiției tensorului Ricci R 0ctv = g xctctr xctr (etapa 3) și prin redenumirea indicilor (etapa 4), obținem
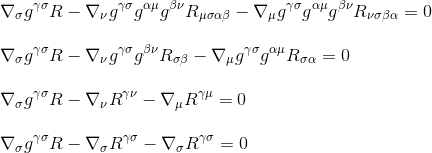
prin factorizarea derivatului, obținem în cele din urmă
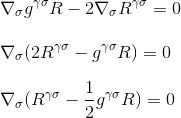
ceea ce este exact ceea ce am vrut să demonstrăm: divergența tensorului Einstein este nulă și am găsit candidatul potrivit pentru partea stângă a ecuației noastre de curbură/masă-energie.