Bittioperaatio

bittisiirtoja pidetään joskus bittioperaatioina, koska ne käsittelevät arvoa bittien sarjana eikä numeerisena suureena. Näissä operaatioissa numeroita siirretään vasemmalle tai oikealle. Tietokoneen suorittimen rekisterit ovat tasalevyisiä, joten jotkin bitit ”siirretään” rekisteristä toiseen päähän, kun taas sama määrä bittejä ”siirretään” toisesta päästä; erot bittien siirtymisoperaattoreiden välillä ovat siinä, miten ne määrittävät siirtyneiden bittien arvot.

Bit adjustingedit

jos rekisterin leveys (usein 32 tai jopa 64) on suurempi kuin pienimmän osoitettavan yksikön (atomielementti), jota usein kutsutaan tavuksi, bittien määrä (yleensä 8), shift-operaatiot aiheuttavat osoitejärjestelmän biteille.Rekisterin molemmissa päissä olevista rajavaikutuksista piittaamatta aritmeettiset ja loogiset shift-operaatiot käyttäytyvät samalla tavalla, ja 8-bittisellä positiolla tapahtuva vaihto kuljettaa bittikuvion 1-tavuisella positiolla seuraavalla tavalla:

aritmeettinen shiftedit

vasen aritmeettinen vaihto

oikea aritmeettinen vaihto

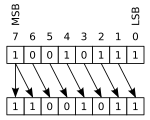
aritmeettisessa siirrossa kummastakin päästä siirretyt bitit hylätään. Vasemmanpuoleisessa aritmeettisessa siirrossa nollia siirretään oikealle; oikeassa aritmeettisessa siirrossa merkkibitti (MSB kahden komplementissa)siirtyy vasemmalle, jolloin operandin merkki säilyy.

tässä esimerkissä käytetään 8-bittistä rekisteriä, joka tulkitaan kahden komplementiksi:

 00010111 (decimal +23) LEFT-SHIFT= 00101110 (decimal +46)

 10010111 (decimal −105) RIGHT-SHIFT= 11001011 (decimal −53)

ensimmäisessä tapauksessa vasemmanpuoleisin numero siirrettiin rekisterin lopun ohi, ja uusi 0 siirrettiin oikeanpuoleisimmalle paikalle. Toisessa tapauksessa oikeanpuoleisin 1 siirrettiin pois (ehkä kantolippuun), ja uusi 1 kopioitiin vasemmanpuoleisimpaan asentoon, jolloin numeron merkki säilyi. Useita vuoroja lyhennetään joskus yhteen vuoroon jollakin numeromäärällä. Esimerkiksi:

 00010111 (decimal +23) LEFT-SHIFT-BY-TWO= 01011100 (decimal +92)

vasen aritmeettinen muutos n vastaa kertomista 2n: llä (edellyttäen, että arvo ei ylivuotoa), kun taas oikea aritmeettinen muutos n: llä kahden komplementin arvosta vastaa jakamista 2n: llä ja pyöristämistä kohti negatiivista äärettömyyttä. Jos binäärilukua käsitellään Ykkösen komplementtina, niin sama oikeasiirtymisoperaatio johtaa jakoon 2n: llä ja pyöristykseen kohti nollaa.

looginen shiftEdit

vasen looginen vaihto

oikea looginen siirto

loogisessa siirrossa nollia siirretään poistettujen bittien tilalle. Näin ollen loogiset ja aritmeettiset vasemmanpuoleiset siirtymät ovat täsmälleen samat.

koska looginen right-shift lisää arvon 0 bittiä merkittävimpään bittiin, se sopii merkkibitin kopioimisen sijaan allekirjoittamattomille binääriluvuille, kun taas aritmeettinen oikeasiirtymä sopii allekirjoitettujen kahden komplementin binääriluvuille.

Ympyränmuutos

toinen vuoron muoto on ympyränmuutos, bitwise-kierto tai bittikierto.

RotateEdit

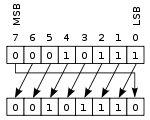vasen Pyöreä siirto tai kierrä

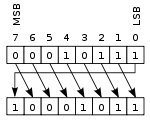Oikea pyöreä siirto tai kiertää

tässä operaatiossa, jota joskus kutsutaan kiertämään ei kuljettaa, bittiä ”pyöritetään” ikään kuin rekisterin vasen ja oikea pää olisivat yhdistyneet. Arvo, joka on siirretty oikealle aikana vasemmalle-shift on mitä arvo on siirretty pois vasemmalle, ja päinvastoin oikeanpuoleisen shift-operaation. Tämä on hyödyllistä, jos on tarpeen säilyttää kaikki olemassa olevat bitit, ja sitä käytetään usein digitaalisessa salauksessa.

Kierrä carryeditin läpi

vasen kiertää kantoliikkeen läpi

oikea kierrä kantaman läpi

Rotate through carry on muunnelma pyöritysoperaatiosta, jossa bitti, joka siirretään sisään (kummassakin päässä) on kantolipun Vanha arvo, ja bitti, joka siirretään ulos (toisessa päässä), tulee kantolipun uudeksi arvoksi.

yksi kierros kantolipun kautta voi simuloida yhden paikan loogista tai aritmeettista siirtymistä asettamalla kantolipun etukäteen. Esimerkiksi jos kantolipussa on 0, niin x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE on looginen oikeistosiirtymä, ja jos kantolipussa on kopio merkkibitistä, niin x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE on aritmeettinen oikeistosiirtymä. Tästä syystä jotkut mikrokontrollerit, kuten halvimmat kuvat, ovat vain kiertävät ja kiertävät kuljettavat, eivätkä vaivaudu aritmeettisiin tai loogisiin vaihto-ohjeisiin.

Rotation through carry on erityisen hyödyllinen suoritettaessa siirtoja määrille, jotka ovat suurempia kuin prosessorin natiivin sanakoko, koska jos suuri luku tallennetaan kahteen rekisteriin, ensimmäisen rekisterin toisesta päästä pois siirtyvän bitin on tultava toisen päähän. Pyörivä läpi-carry, että bitti on ”tallennettu” carry lippuun Ensimmäisen vuoron aikana, valmis siirtymään toisen vuoron aikana ilman ylimääräisiä valmisteluja.

korkean tason kielilläedit

C-familyEdit

C-perhekielissä loogiset vuoronhaltijat ovat ”<<” vasemmalle vuorolle ja ”>>” oikealle vuorolle. Toiseksi argumentiksi operaattorille ilmoitetaan vaihtopaikkojen määrä. Esimerkiksi,

x = y << 2;

määrittää x tuloksen, jossa y siirtyy vasemmalle kahdella bitillä, mikä vastaa kertolaskua neljällä.

muutokset voivat johtaa toteutuksessa määriteltyyn käyttäytymiseen tai määrittelemättömään käyttäytymiseen, joten niitä käytettäessä on noudatettava varovaisuutta. Tuloksena siirtymisestä bittimäärällä, joka on suurempi tai yhtä suuri kuin sanan koko, on määrittelemätön käyttäytyminen C: ssä ja C++: ssa. Oikealle siirtyvä negatiivinen arvo on toteutus-määritelty eikä sitä suositella hyvän koodauskäytännön mukaan; vasemmalle siirtyvän allekirjoitetun arvon tulos on määrittelemätön, jos tulosta ei voida esittää tulostyypissä.

C#: ssa oikeasiirtymä on aritmeettinen siirtymä, kun ensimmäinen operandi on int tai pitkä. Jos ensimmäinen operandi on tyypiltään uint tai ulong, on oikeasiirtymä looginen Siirtymä.

Kiertovaihteisto

C-kieliperheestä puuttuu kääntöoperaattori, mutta sellainen voidaan syntetisoida vaihtooperaattoreista. On huolehdittava siitä, että lausunto on hyvin muodostettu, jotta vältetään määrittelemätön käyttäytyminen ja ajoitus hyökkäyksiä ohjelmisto tietoturvavaatimuksia. Esimerkiksi naiivi toteutus, joka jätti kiertämättä 32-bittisen allekirjoittamattoman arvon x n asemilla, on yksinkertaisesti:

uint32_t x = ..., n = ...;uint32_t y = (x << n) | (x >> (32 - n));

0 bittien muutos johtaa kuitenkin määrittelemättömään käyttäytymiseen oikean käden lausekkeessa (x >> (32 - n)), koska 32 - 0 on 32, ja 32 on alueen ulkopuolella. Toinen yritys voi johtaa:

uint32_t x = ..., n = ...;uint32_t y = n ? (x << n) | (x >> (32 - n)) : x;

jossa shift määrä testataan sen varmistamiseksi, että se ei käyttöön määrittelemätön käyttäytyminen. Haara kuitenkin lisää ylimääräisen koodipolun ja tarjoaa mahdollisuuden ajoituksen analysointiin ja hyökkäykseen, mikä ei usein ole hyväksyttävää korkean eheyden ohjelmistossa. Lisäksi koodi kokoaa yhteen useita koneen ohjeita, mikä on usein tehottomampaa kuin prosessorin natiiviohje.

määrittelemättömän käyttäytymisen ja GCC: n alaisten haarojen välttämiseksi suositellaan seuraavaa. Kuvion tunnistaa moni kääntäjä, ja kääntäjä lähettää yhden pyörimisohjeen:

uint32_t x = ..., n = ...;uint32_t y = (x << n) | (x >> (-n & 31));

on myös kääntäjäkohtaisia sisäsivuja, jotka toteuttavat pyöreitä siirtymiä, kuten _rotl8, _rotl16, _rotr8, _rotr16 Microsoft Visual C++: ssa. Clang tarjoaa joitakin kiertää luontainen Microsoft yhteensopivuus, joka kärsii ongelmista edellä. GCC ei tarjoa kiertäviä luontaisia ominaisuuksia. Intel tarjoaa myös x86 Intrinsicejä.

JavaEdit

Jaavassa kaikki kokonaislukutyypit merkitään, joten ”<<” ja ”>>” – operaattorit suorittavat aritmeettisia siirtymiä. Java lisää operaattorin” >>> ”suorittamaan loogisia oikeanpuoleisia siirtoja, mutta koska loogiset ja aritmeettiset vasemmanpuoleiset operaatiot ovat identtisiä allekirjoitetulle kokonaisluvulle, Ei Javassa ole” <<< ” -operaattoria.

lisätietoja Java shift-operaattoreista:

• operaattoreita << (vasen vuoro), >> (allekirjoitettu oikea vuoro) ja >>> (allekirjoittamaton oikea vuoro) kutsutaan vuorooperaattoreiksi.
• vaihtoilmaisun tyyppi on vasemmanpuoleisen operandin ylennetty tyyppi. Esimerkiksi aByte >>> 2 vastaa ((int) abytea) >>> 2.
• jos vasemmanpuoleisen operandin ylennetty tyyppi on int, vuorovälinä käytetään vain oikeanpuoleisen operandin viittä alimman kertaluvun bittiä. Aivan kuin oikeanpuoleinen operandi olisi Alistettu bitwise-loogiselle ja operaattorille & maskiarvolla 0x1f (0b11111). Todellisuudessa käytetty vuoroetäisyys on siis aina välillä 0-31, mukaan lukien.
• jos vasemmanpuoleisen operandin ylennetty tyyppi on pitkä, vuorovälinä käytetään vain oikeanpuoleisen operandin kuutta alimman kertaluvun bittiä. Aivan kuin oikeanpuoleinen operandi olisi Alistettu bitwise-loogiselle ja operaattorille & maskiarvolla 0x3f (0b111111). Todellisuudessa käytetty vuoroetäisyys on siis aina välillä 0-63, mukaan lukien.
• n >>> s arvo on n oikealle siirtyneitä s-bittejä, joissa on nolla-laajennus.
• bit-ja shift-operaatioissa tyyppi byte muunnetaan implisiittisesti muotoon int. Jos tavuarvo on negatiivinen, korkein bitti on yksi, niin ykkösiä käytetään täyttämään ylimääräiset tavut int: ssä. Niinpä tavu b1 = -5; int i = b1 | 0x0200; tuloksena on i == -5.

JavaScriptEdit

JavaScript käyttää bitwise-operaatioita arvioidakseen jokaisen kahdesta tai useammasta yksiköstä paikan 1 tai 0.

PascalEdit

Pascalissa, samoin kuin kaikissa sen murteissa (kuten Object Pascal ja Standard Pascal), loogiset vasemman ja oikean vaihtooperaattorit ovat vastaavasti ”shl” ja ”shr”. Myös allekirjoitetuilla kokonaisluvuilla shr käyttäytyy loogisen siirtymän tavoin, eikä kopioi merkkibittiä. Toisena argumenttina on vuoropaikkojen määrä. Esimerkiksi seuraava antaa X: lle tuloksen, jossa y siirtyy vasemmalle kahdella bitillä:

x := y shl 2;