intervalele Interquartile și valorile aberante

• Purplemath
• MathHelp.com
• găsiți valorile aberante, dacă există, pentru următorul set de date:
• găsiți valorile aberante și extreme, dacă există, pentru următorul set de date și desenați graficul box-and-whisker. Marcați orice valori aberante cu un asterisc și orice valori extreme cu un punct deschis.

Purplemath

„gama interquartile”, prescurtată „IQR”, este doar lățimea cutiei din complotul box-and-whisker. Adică IQR = Q3-Q1 . IQR poate fi folosit ca o măsură a modului în care sunt răspândite valorile.

Statisticile presupun că valorile dvs. sunt grupate în jurul unei valori centrale. IQR spune cât de răspândite sunt valorile ” medii; de asemenea, poate fi folosit pentru a spune când unele dintre celelalte valori sunt „prea departe” de valoarea centrală. Aceste puncte ” prea îndepărtate „sunt numite” valori aberante”, deoarece” se află în afara ” intervalului în care le așteptăm.

IQR este lungimea cutiei din complotul dvs. Un outlier este orice valoare care se află de mai mult de o dată și jumătate lungimea cutiei de la fiecare capăt al cutiei.

conținutul continuă mai jos

MathHelp.com

adică, dacă un punct de date este sub Q1-1,5 IQR sau peste Q3 + 1,5 IQR IQR, este considerat ca fiind prea departe de valorile centrale pentru a fi rezonabil. Poate ai lovit cântarul când ai făcut acea măsurătoare, sau poate partenerul tău de laborator este un idiot și nu ar fi trebuit să-l lași să atingă vreun echipament. Cine știe? Dar oricare ar fi cauza lor, valorile aberante sunt acele puncte care nu par să se „potrivească”.

odată ce vă simțiți confortabil să găsiți IQR, puteți trece la localizarea valorilor aberante, dacă există.

• găsiți valorile aberante, dacă există, pentru următorul set de date:

valorile pentru Q1-1.5 IQR si Q3 + 1.5 IQR sunt ” gardurile „care marcheaza valorile” rezonabile ” din valorile outlier. Valorile aberante se află în afara gardurilor.

dacă misiunea dvs. vă pune să luați în considerare nu numai valorile aberante, ci și „valorile extreme”, atunci valorile pentru Q1 – 1.5 IQR si Q3 + 1,5 IQR sunt gardurile „interioare”, iar valorile pentru Q1 – 3 IQR si Q3 + 3 IQR sunt gardurile „exterioare”.

valorile aberante (marcate cu asteriscuri sau puncte deschise) se află între gardurile interioare și exterioare, iar valorile extreme (marcate cu oricare simbol pe care nu l-ați folosit pentru valorile aberante) se află în afara gardurilor exterioare.

apropo, cartea dvs. se poate referi la valoarea „1,5 IQR-uri de la sută” ca fiind un „pas”. Apoi valorile aberante vor fi numerele care se află între unul și doi pași de la balamale, iar valoarea extremă va fi numerele care sunt la mai mult de doi pași de balamale.

privind din nou la exemplul anterior, gardurile exterioare ar fi la 14.4 – 3 0.5 = 12.9 și 14.9 + 3 0.5 = 16.4. Deoarece 16.4 este chiar pe gardul exterior superior, Acest lucru ar fi considerat a fi doar o valoare outlier, nu o valoare extremă. Dar 10.2 este complet sub gardul exterior inferior, deci 10.2 ar fi o valoare extremă.

calculatorul dvs. grafic poate indica sau nu dacă un complot box-and-whisker include valori aberante. De exemplu, problema de mai sus include punctele 10.2, 15.9 și 16.4 ca valori aberante. O setare pe calculatorul meu grafic oferă simplu complot box-and-whisker care utilizează doar rezumatul cinci numere, astfel încât cele mai îndepărtate valori aberante sunt prezentate ca fiind punctele finale ale mustati:

o setare diferită calculator dă caseta-și-mustăți complot cu valorile aberante special marcate (în acest caz, cu o simulare a unui punct deschis), și mustăți merge doar în măsura în care cele mai mari și cele mai mici valori care nu sunt valori aberante:

calculatorul meu nu face nicio distincție între valori aberante și valori extreme. Nici a ta nu poate. Verificați manualul proprietarului acum, înainte de următorul test.

dacă utilizați calculatorul grafic pentru a vă ajuta cu aceste parcele, asigurați-vă că știți ce setare ar trebui să utilizați și ce înseamnă rezultatele sau calculatorul vă poate oferi un răspuns perfect corect, dar „greșit”.

• găsiți valorile aberante și extreme, dacă există, pentru următorul set de date și desenați graficul box-and-whisker. Marcați orice valori aberante cu un asterisc și orice valori extreme cu un punct deschis.

publicitate

pentru a găsi valorile aberante și extreme, trebuie mai întâi să găsească IQR. Deoarece există șapte valori în listă, mediana este a patra valoare, deci:

Q2 = 25

prima jumătate a listei este:

21, 23, 24

…deci Q1 = 23; a doua jumătate este:

29, 33, 49

…deci Q3 = 33. Apoi IQR este dat de:

IQR = 33 – 23 = 10

valorile aberante vor fi orice valori de mai jos:

23 – 1.5×10 = 23 – 15 = 8

…sau mai sus:

33 + 1.5×10 = 33 + 15 = 48

valorile extreme vor fi cele de mai jos:

23 – 3×10 = 23 – 30 = -7

…sau mai sus:

33 + 3×10 = 33 + 30 = 63

deci, am un outlier la 49, dar nu există valori extreme. Nu voi avea o mustață de top pe complotul meu, deoarece Q3 este, de asemenea, cel mai mare non-outlier. Deci complotul meu arată astfel:

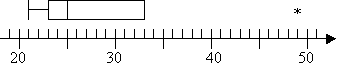
trebuie remarcat faptul că metodele, termenii și regulile prezentate mai sus sunt ceea ce am învățat și ceea ce am văzut cel mai frecvent învățat. Cu toate acestea, cursul dvs. poate avea reguli specifice diferite sau calculatorul dvs. poate face calcule ușor diferit. Este posibil să fie nevoie să fii oarecum flexibil în găsirea răspunsurilor specifice curriculumului tău.