powrót do indeksu lekcji | Uporządkuj lekcje / strona przyjazna do wydruku
Logarytmy: Wprowadzenie do
„relacja” (strona 1 z 3)
działy: Wprowadzenie do logów, upraszczanie wyrażeń logarytmów, dzienniki zwykłe i naturalne
Logarytmy są „przeciwieństwem” wykładników, tak jak odejmowanie jest przeciwieństwem dodawania, a dzielenie jest przeciwieństwem mnożenia. Rejestruje” Cofnij ” wykładniki. Technicznie rzecz biorąc, dzienniki są odwrotnością wykładników.
w praktyce uważam, że warto myśleć o logach w kategoriach relacji:
| —relacja— | |||
|
po lewej stronie Powyżej znajduje się wykładnicze stwierdzenie „y = bx”. Po prawej stronie powyżej, „logb (y) = x” jest równoważnym wyrażeniem logarytmicznym, które wymawia się „log-base-b z y równa się x”; wartość subskryptu ” b „jest” podstawą logarytmu”, podobnie jak B jest podstawą w wyrażeniu wykładniczym”bx”. I tak jak podstawa B w wykładniku jest zawsze dodatnia i nie równa 1, tak również podstawa b Dla logarytmu jest zawsze dodatnia i nie równa 1. Cokolwiek znajduje się wewnątrz logarytmu, nazywa się „argumentem” logarytmu. Zauważ, że baza zarówno w równaniu wykładniczym, jak i równaniu logarytmicznym (powyżej) wynosi „b”, ale x I y zmieniają strony, gdy przełączasz się między dwoma równaniami.
—relacja Animowana—
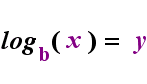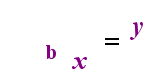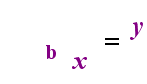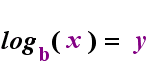
jeśli pamiętasz tę relację (że cokolwiek było argumentem logarytmu staje się” równe”, a cokolwiek było” równe ” staje się wykładnikiem w wykładniku i odwrotnie), to nie powinieneś mieć zbyt wielu problemów z logarytmami.
(sam ukułem termin „związek”. Nie znajdziesz go w swoim tekście, a twoi nauczyciele i nauczyciele nie będą mieli pojęcia, o czym mówisz, jeśli im o tym wspomnisz. „Związek” jest całkowicie niestandardową terminologią. Dlaczego w ogóle go używam? Bo to działa.)
przy okazji: jeśli zauważyłeś, że zmieniłem zmienne między dwoma polami wyświetlającymi „relację”, masz ostre oko. Zrobiłem to celowo, aby podkreślić, że nie chodzi o same zmienne, ale o to, jak się poruszają.
- Konwertuj „63 = 216” na równoważne wyrażenie logarytmiczne.
aby przekonwertować, podstawa (czyli 6)pozostaje taka sama, ale 3 i 216 zmieniają strony. To daje mi:
log6(216) = 3 Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
- Konwertuj „log4(1024) = 5” na równoważne wyrażenie wykładnicze.
aby przekonwertować, podstawa (czyli 4) pozostaje taka sama, ale 1024 i 5 zmieniają strony. To daje mi:
45 = 1024
Top| 1 | 2 | 3 | wróć do indeksu następny >>
|
Przytocz ten artykuł jako: |
Stapel Elżbieta „Logarytmy: Wprowadzenie do 'relacji’.”Purplemath. Dostępne od 2016
|