
















Timsort: bardzo szybki , O(N log n), stabilny algorytm sortowania zbudowany dla świata rzeczywistego — Nie skonstruowany w środowisku akademickim.
Kliknij tutaj, aby wyświetlić zaktualizowany artykuł:

Timsort jest algorytmem sortującym, który jest wydajny dla rzeczywistych danych i nie jest tworzony w laboratorium akademickim. Tim Peters stworzył Timsort dla języka programowania Python w 2001 roku. Timsort najpierw analizuje listę, którą próbuje posortować, a następnie wybiera podejście oparte na analizie listy.
od czasu wynalezienia algorytmu jest on używany jako domyślny algorytm sortowania w Pythonie, Javie, na platformie Android i w GNU Octave.
Wielka notacja o Timsorta to O (N log N). Aby dowiedzieć się więcej o notacji Big O, przeczytaj to.

czas sortowania Timsort jest taki sam jak Mergesort, który jest szybszy niż większość innych rodzajów, które możesz znać. Timsort faktycznie korzysta z Insertion sort i Mergesort, jak wkrótce zobaczysz.
Peters zaprojektował Timsort tak, aby używał już uporządkowanych elementów, które istnieją w większości rzeczywistych zestawów danych. Nazywa te już uporządkowane elementy „naturalnymi przebiegami”. Iteracje nad danymi zbierając elementy do uruchomień i jednocześnie łącząc te uruchomienia razem w jeden.
tablica ma mniej niż 64 elementy
jeśli tablica, którą próbujemy posortować, ma mniej niż 64 elementy, Timsort wykona sortowanie wstawiania.
sortowanie wstawiania jest prostym sortowaniem, które jest najbardziej skuteczne na małych listach. Jest dość powolny na większych listach, ale bardzo szybki przy małych listach. Idea sortowania wstawiania jest następująca:
- spójrz na elementy jeden po drugim
- Zbuduj posortowaną listę, wstawiając element w odpowiednim miejscu
oto tabela śledzenia pokazująca, jak sortowanie wstawiania posortuje listę

w tym przypadku wstawiamy nowo posortowane elementy do nowej pod-tablicy, która rozpoczyna się na początku tablicy.
oto gif pokazujący wstawianie:
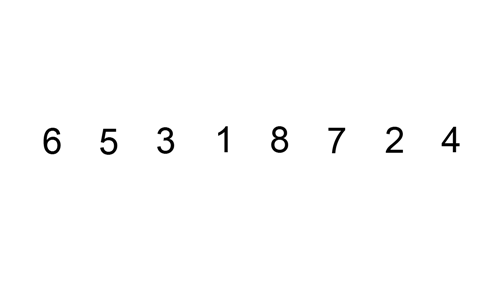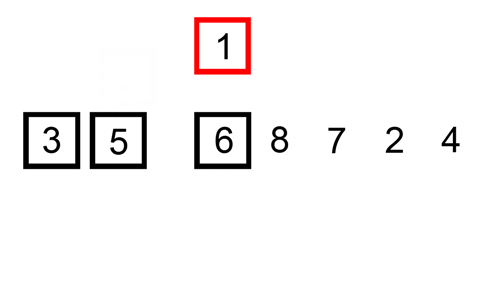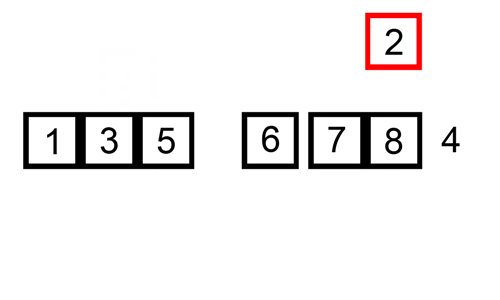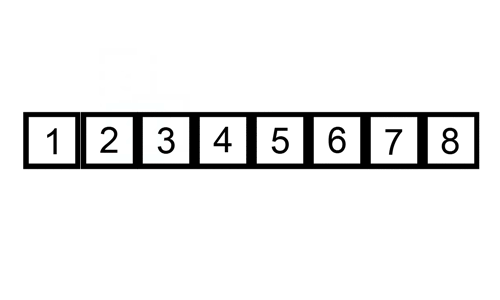
więcej o uruchomieniach
jeśli lista jest większa niż 64 elementy, algorytm pierwszy przejdzie przez Listę szukając części, które są ściśle wzrastające lub malejące. Jeśli część maleje, odwróci tę część.
więc jeśli bieg maleje, będzie wyglądał tak (gdzie bieg jest pogrubiony):

jak nie maleje to bedzie wygladac tak:

minrun jest wielkością, która jest określana na podstawie wielkości tablicy. Algorytm wybiera go tak, że większość uruchomień w losowej tablicy ma lub ma długość minrun. Scalanie 2 tablic jest bardziej wydajne, gdy liczba uruchomień jest równa lub nieco mniejsza od potęgi dwóch. Timsort wybiera minrun, aby spróbować zapewnić tę wydajność, upewniając się, że minrun jest równy lub mniejszy od potęgi dwójki.
algorytm wybiera minrun z zakresu od 32 do 64 włącznie. Wybiera minrun w taki sposób, że długość oryginalnej tablicy, po podzieleniu przez minrun, jest równa lub nieco mniejsza od potęgi dwójki.
jeśli długość biegu jest mniejsza niż minrun, oblicza się długość tego biegu z minrun. Korzystając z tego nowego numeru, pobierasz wiele elementów przed biegiem i wykonujesz sortowanie wstawiania, aby utworzyć nowy bieg.
więc jeśli minrun ma 63, A długość biegu wynosi 33, robisz 63-33 = 30. Następnie pobierasz 30 elementów przed końcem biegu, więc jest to 30 elementów z biegu, a następnie wykonujesz sortowanie wstawiania, aby utworzyć nowy bieg.
po zakończeniu tej części powinniśmy mieć teraz kilka posortowanych uruchomień na liście.

Timsort wykonuje teraz mergesort, aby scalić biegi razem. Jednak Timsort dba o zachowanie stabilności i scalanie równowagi podczas sortowania scalającego.
aby utrzymać stabilność nie powinniśmy wymieniać 2 liczb o równej wartości. To nie tylko utrzymuje ich oryginalne pozycje na liście, ale umożliwia szybsze działanie algorytmu. Wkrótce omówimy balans merge.
gdy Timsort znajduje biegi, dodaje je do stosu. Prosty stos wyglądałby tak:

wyobraź sobie stos talerzy. Nie możesz brać talerzy od dołu, więc musisz wziąć je od góry. To samo dotyczy stosu.
Timsort próbuje zrównoważyć dwie konkurencyjne potrzeby podczas uruchamiania mergesort. Z jednej strony chcielibyśmy opóźnić łączenie tak długo, jak to możliwe, aby wykorzystać wzorce, które mogą pojawić się później. Ale chcielibyśmy jeszcze bardziej zrobić połączenie jak najszybciej, aby wykorzystać run, który właśnie znaleziony run jest nadal wysoko w hierarchii pamięci. Nie możemy również opóźniać scalania „zbyt długo”, ponieważ zużywa pamięć, aby zapamiętać biegi, które są nadal niezabezpieczone, a stos ma stały rozmiar.
aby upewnić się, że mamy ten kompromis, Timsort śledzi trzy najnowsze elementy na stosie i tworzy dwa prawa, które muszą być prawdziwe dla tych elementów:
1. A > B + C
2. B > C
gdzie A, B I C to trzy ostatnie pozycje na stosie.
słowami samego Tima Petersa:
to, co okazało się dobrym kompromisem, utrzymuje dwie niezmienniki na wpisach stosu, gdzie A, B I C są długościami trzech prawych, jeszcze nie połączonych plastrów
Zwykle łączenie sąsiednich przebiegów o różnych długościach w miejscu jest trudne. Jeszcze trudniej jest utrzymać stabilność. Aby to obejść, Timsort odkłada tymczasową pamięć. Umieszcza mniejsze (wywołujące obie trasy a i B) z dwóch tras w tej pamięci tymczasowej.
galopujący

podczas gdy Timsort łączy A i B, zauważa, że jeden bieg „wygrywał” wiele razy z rzędu. Gdyby okazało się, że bieg A składał się z całkowicie mniejszych liczb niż bieg B, to bieg a skończyłby z powrotem na swoim pierwotnym miejscu. Połączenie obu biegów wymagałoby wiele pracy, aby nic nie osiągnąć.
częściej niż nie, Dane będą miały wcześniej istniejącą strukturę wewnętrzną. Timsort zakłada, że jeśli wiele wartości run a jest niższych od wartości run B, to jest prawdopodobne, że A będzie nadal miało mniejsze wartości niż B.
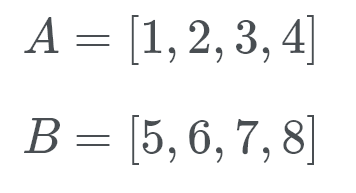
Timsort wejdzie w tryb galopowania. Zamiast sprawdzać A i B względem siebie, Timsort wykonuje binarne wyszukiwanie odpowiedniej pozycji b w a. w ten sposób Timsort może przenieść całą sekcję a na miejsce. Następnie Timsort wyszukuje odpowiednią lokalizację a w B. Timsort następnie przeniesie całą sekcję B can na raz i na miejsce.
zobaczmy to w akcji. Timsort sprawdza B (co jest 5) i używając wyszukiwania binarnego szuka poprawnej lokalizacji w A.
Cóż, B należy na końcu listy A. Teraz Timsort sprawdza A (co jest 1) w prawidłowej lokalizacji B. więc szukamy, gdzie idzie liczba 1. Ta liczba idzie na początku B. Teraz wiemy, że B należy na końcu A i a należy na początku B.
okazuje się, że ta operacja nie jest tego warta, jeśli odpowiednia lokalizacja dla B jest bardzo blisko początku A (lub odwrotnie). tryb galopu szybko wychodzi, jeśli się nie opłaca. Dodatkowo, Timsort zauważa i utrudnia wejście do trybu galopu później, zwiększając liczbę kolejnych zwycięstw tylko A lub tylko B wymaganych do wejścia. Jeśli tryb galopu się opłaca, Timsort ułatwia powrót.
krótko mówiąc, Timsort robi 2 rzeczy niesamowicie dobrze:
- świetna wydajność na tablicach z wcześniej istniejącą strukturą wewnętrzną
- będąc w stanie utrzymać stabilny sortowanie
wcześniej, aby uzyskać stabilne sortowanie, musisz spakować elementy na liście za pomocą liczb całkowitych i posortować je jako tablicę krotek.
Kod
jeśli nie jesteś zainteresowany kodem, możesz pominąć tę część. Poniżej znajduje się więcej informacji.
poniższy kod źródłowy jest oparty na pracy mojej i Nanda Javarma. Kod źródłowy nie jest kompletny, ani nie jest podobny do oficjalnego kodu źródłowego sorted () Pythona. To jest po prostu głupi Timsort, który zaimplementowałem, aby uzyskać ogólne odczucie Timsorta. Jeśli chcesz zobaczyć oryginalny kod źródłowy Timsort w całej okazałości, sprawdź go tutaj. Timsort jest oficjalnie zaimplementowany w języku C, a nie Python.
Timsort jest w rzeczywistości wbudowany w Pythona, więc ten kod służy tylko jako wyjaśnienie. Aby korzystać z Timsort wystarczy napisać:
list.sort()
lub
sorted(list)
jeśli chcesz opanować, jak działa Timsort i poczuć go, zdecydowanie sugeruję, abyś spróbował go zaimplementować!
ten artykuł jest oparty na oryginalnym wstępie Tima Petersa do Timsort, znalezionym tutaj.