
















Timsort: un algoritm de sortare foarte rapid , O(n log n), stabil, construit pentru lumea reală — nu construit în mediul academic.
Click aici pentru a vedea articolul actualizat:

Timsort este un algoritm de sortare care este eficient pentru datele din lumea reală și nu este creat într-un laborator academic. Tim Peters a creat Timsort pentru limbajul de programare Python în 2001. Timsort analizează mai întâi lista pe care încearcă să o sorteze și apoi alege o abordare bazată pe analiza listei.
de când algoritmul a fost inventat, acesta a fost folosit ca algoritm de sortare implicit în Python, Java, platforma Android și în GNU Octave.
notația o mare a lui Timsort este O(n log n). Pentru a afla despre notația Big O, citiți acest lucru.

timpul de sortare al Timsort este același cu Mergesort, care este mai rapid decât majoritatea celorlalte tipuri pe care le-ați putea cunoaște. Timsort folosește de fapt sortarea inserției și Mergesort, așa cum veți vedea în curând.
Peters a proiectat Timsort pentru a utiliza elemente deja ordonate care există în majoritatea seturilor de date din lumea reală. El numește aceste elemente deja ordonate „alergări naturale”. Iterează peste datele care colectează elementele în rulări și fuzionează simultan acele rulări împreună într-una.
matricea are mai puțin de 64 de elemente în ea
dacă matricea pe care încercăm să o sortăm are mai puțin de 64 de elemente în ea, Timsort va executa o sortare de inserare.
un fel de inserare este un fel simplu, care este cel mai eficient pe liste mici. Este destul de lent la liste mai mari, dar foarte rapid cu liste mici. Ideea unui fel de inserție este după cum urmează:
- Uită-te la elemente unul câte unul
- construi lista sortate prin introducerea elementului la locația corectă
Iată un tabel de urmărire care arată modul de sortare Inserare ar sorta lista

în acest caz, vom insera elementele nou sortate într-un nou sub-matrice, care începe la începutul matrice.
Iată un gif care arată sortarea inserției:
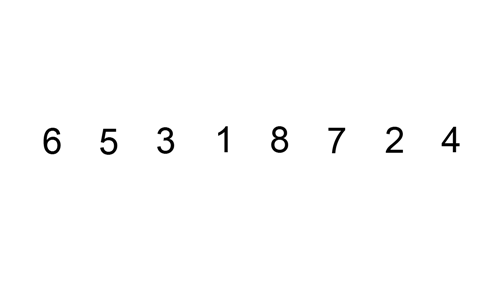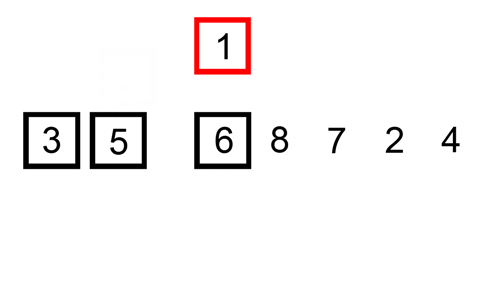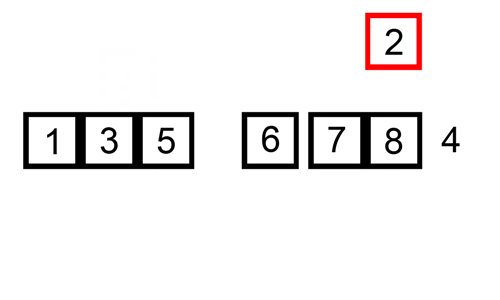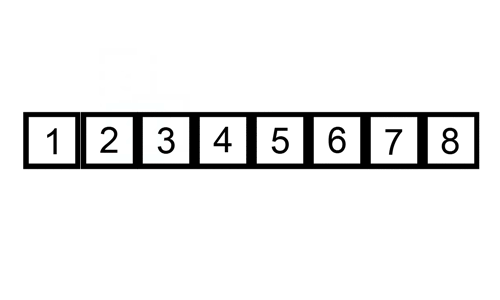
mai multe despre ruleaza
în cazul în care lista este mai mare de 64 de elemente decât algoritmul va face o primă trecere prin lista caută piese care sunt strict în creștere sau în scădere. Dacă partea este în scădere, se va inversa acea parte.
deci, dacă rularea scade, va arăta astfel (unde Rularea este cu caractere aldine):

dacă nu scade, va arăta astfel:

minrun este o dimensiune care este determinată pe baza dimensiunii matrice. Algoritmul îl selectează astfel încât majoritatea rulărilor dintr-o matrice aleatorie să aibă sau să devină minrun, în lungime. Îmbinarea a 2 matrice este mai eficientă atunci când numărul de rulări este egal sau puțin mai mic decât o putere de două. Timsort alege minrun pentru a încerca să asigure această eficiență, asigurându-se că minrun este egal sau mai mic decât o putere de doi.
algoritmul alege minrun din intervalul 32-64 inclusiv. Alege minrun astfel încât lungimea matricei originale, atunci când este împărțită la minrun, este egală sau puțin mai mică decât o putere de două.
dacă lungimea alergării este mai mică decât minrun, calculați lungimea acelei fugi de minrun. Folosind acest număr nou, te apuca că multe elemente înainte de termen și de a efectua un fel de inserție pentru a crea un nou termen.
deci, dacă minrun este 63 și lungimea alergării este 33, faceți 63-33 = 30. Apoi apucați 30 de elemente din fața sfârșitului rulării, deci acestea sunt 30 de elemente din rulare și apoi efectuați un fel de inserare pentru a crea o nouă rulare.
după ce această parte a fost finalizată, ar trebui să avem acum o grămadă de rulări sortate într-o listă.
fuzionare

Timsort efectuează acum mergesort pentru a îmbina rulările împreună. Cu toate acestea, Timsort se asigură că menține stabilitatea și echilibrul de îmbinare în timp ce sortează îmbinarea.
pentru a menține stabilitatea nu ar trebui să schimbăm 2 numere de valoare egală. Acest lucru nu numai că își păstrează pozițiile inițiale în listă, dar permite algoritmului să fie mai rapid. În scurt timp vom discuta despre bilanțul fuziunii.
pe măsură ce Timsort găsește rulează, le adaugă la o stivă. O stivă simplă ar arăta astfel:

Imaginați-vă un teanc de plăci. Nu puteți lua farfurii de jos, așa că trebuie să le luați de sus. Același lucru este valabil și despre o stivă.
Timsort încearcă să echilibreze două nevoi concurente atunci când mergesort rulează. Pe de o parte, am dori să amânăm fuzionarea cât mai mult timp posibil pentru a exploata tiparele care pot apărea mai târziu. Dar ne-ar plăcea și mai mult să facem fuziunea cât mai curând posibil pentru a exploata rularea pe care tocmai a găsit-o este încă ridicată în ierarhia memoriei. De asemenea, nu putem întârzia fuzionarea „prea lungă”, deoarece consumă memorie pentru a-și aminti rulările care sunt încă nemergate, iar stiva are o dimensiune fixă.
pentru a ne asigura că avem acest compromis, Timsort ține evidența celor mai recente trei elemente din stivă și creează două legi care trebuie să fie valabile pentru acele elemente:
1. A > B + C
2. B > C
unde A, B și C sunt cele mai recente trei elemente din stivă.
în cuvintele lui Tim Peters însuși:
ceea ce s-a dovedit a fi un compromis bun menține doi invarianți pe intrările stivei, unde A, B și C sunt lungimile celor trei felii din dreapta care nu au fost încă îmbinate
de obicei, îmbinarea rulărilor adiacente de lungimi diferite în loc este greu. Ceea ce face și mai greu este că trebuie să menținem stabilitatea. Pentru a evita acest lucru, Timsort pune deoparte memoria temporară. Plasează cele mai mici (apelând ambele rulări A și B) dintre cele două rulări în acea memorie temporară.
galop

în timp ce Timsort fuzionează A și B, observă că o alergare a „câștigat” de multe ori la rând. Dacă s-ar dovedi că rularea A consta din numere complet mai mici decât rularea B, atunci rularea A ar ajunge înapoi la locul său inițial. Fuzionarea celor două runde ar implica multă muncă pentru a nu realiza nimic.
de cele mai multe ori, datele vor avea o structură internă preexistentă. Timsort presupune că dacă o mulțime de valori ale rulării A sunt mai mici decât valorile rulării B, atunci este probabil ca A să continue să aibă valori mai mici decât B.
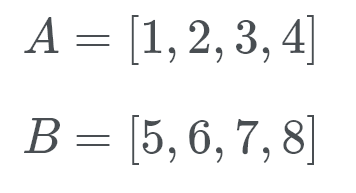
Timsort va intra apoi în modul galop. În loc să verifice A și B unul împotriva celuilalt, Timsort efectuează o căutare binară pentru poziția corespunzătoare a lui b în a.În acest fel, Timsort poate muta o întreagă secțiune a lui a în loc. Apoi Timsort caută locația corespunzătoare A lui A În B. Timsort va muta apoi o întreagă secțiune a cutiei B simultan și în poziție.
să vedem acest lucru în acțiune. Timsort verifică B (care este 5) și folosind o căutare binară caută locația corectă în A.
Ei bine, B aparține în partea din spate a listei A. Acum Timsort verifică A (care este 1) în locația corectă a B. deci, căutăm să vedem unde merge numărul 1. Acest număr merge la începutul lui B. știm acum că B aparține la sfârșitul lui A și A aparține la începutul lui B.
se pare că această operație nu merită dacă locația potrivită pentru B este foarte aproape de începutul lui a (sau invers). deci, modul galop iese rapid dacă nu dă roade. În plus, Timsort ia notă și îngreunează intrarea în modul galop mai târziu prin creșterea numărului de victorii consecutive Doar A sau doar B necesare pentru a intra. Dacă modul gallop dă roade, Timsort facilitează reintroducerea.
pe scurt, Timsort face 2 lucruri incredibil de bine:
- performanță excelentă pe matrice cu structură internă preexistentă
- fiind capabil să mențină un fel stabil
anterior, pentru a obține un fel stabil, ar trebui să zip elementele din lista cu numere întregi, și sortați-l ca o matrice de tupluri.
Cod
dacă nu sunteți interesat de cod, nu ezitați să omiteți această parte. Există mai multe informații sub această secțiune.
codul sursă de mai jos se bazează pe munca mea și Nanda Javarma lui. Codul sursă nu este complet și nici nu este similar cu codul sursă sortat() al Python. Acesta este doar un Timsort prost-jos am implementat pentru a obține o simt generală a Timsort. Dacă doriți să vedeți codul sursă original al Timsort în toată gloria sa, verificați-l aici. Timsort este implementat oficial în C, nu Python.
Timsort este de fapt construit chiar în Python, astfel încât acest cod servește doar ca un explicator. Pentru a utiliza Timsort pur și simplu scrieți:
list.sort()
sau
sorted(list)
dacă doriți să stăpâniți modul în care funcționează Timsort și să vă simțiți, vă sugerez să încercați să îl implementați singur!
acest articol se bazează pe introducerea originală a lui Tim Peters în Timsort, găsită aici.