Zona Moment de inerție – secțiuni transversale tipice i

zona Moment de inerție sau Moment de inerție pentru o zonă – cunoscută și sub numele de al doilea Moment al zonei – I, este o proprietate de formă care este utilizată pentru a prezice deformarea, îndoirea și stresul în grinzi.

zona moment de inerție – unități imperiale

• inches4

zona moment de inerție – unități metrice

• mm4
• cm4
• m4

conversia între unități

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4.16×105 mm4 = 41.6 cm4

exemplu – conversia între momentul zonei de inerție unități

9240 cm4 pot fi convertite în mm4 prin înmulțirea cu 104

(9240 cm4) 104 = 9.24 107 mm4

zonă Moment de inerție (Moment de inerție pentru o zonă sau al doilea Moment de zonă)

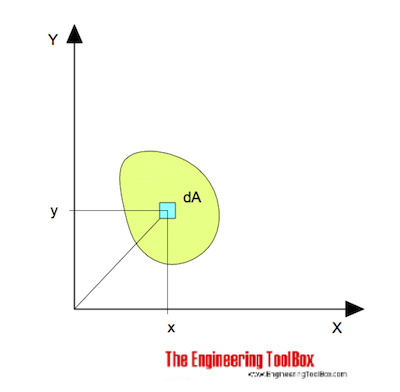
pentru îndoirea în jurul axei x poate fi exprimat ca

Ix = y2 da (1)

unde

Ix = momentul de inerție a zonei în raport cu axa x (m4, mm4, inches4)

y = distanța perpendiculară de la axa X la elementul Da (M, mm, inci)

dA = o suprafață elementară (m2, mm2, inches2)

momentul de inerție pentru îndoire în jurul axei y se poate exprima ca

IY = x2 da (2)

unde

Iy = momentul de inerție al zonei în raport cu axa y (m4, mm4, inchi4)

x = distanța perpendiculară de la axa y la elementul dA (m, mm, inci)

momentul de inerție al zonei pentru secțiunile transversale tipice i

• zonă moment de inerție pentru secțiunile transversale tipice ii

secțiune transversală pătrată solidă

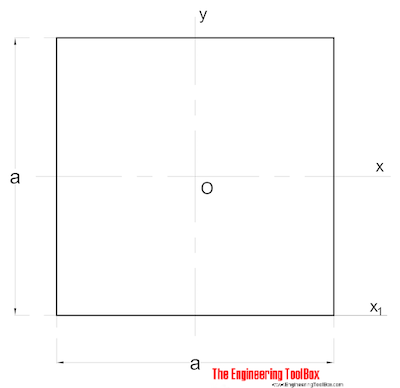
zona moment de inerție pentru o secțiune pătrată solidă poate fi calculată ca

IX = a4 / 12 (2)

unde

a = latură (mm, m, în..)

IY = a4 / 12 (2b)

secțiune transversală dreptunghiulară solidă

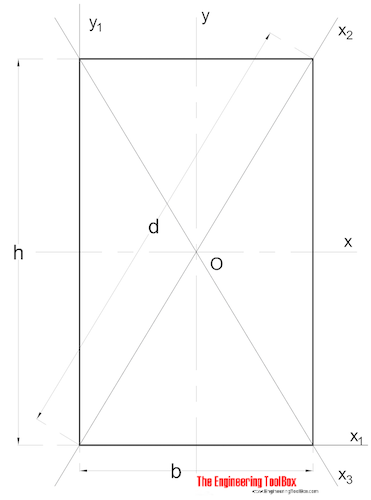
momentul ariei Ineria pentru o secțiune dreptunghiulară poate fi calculat ca

Ix = b h3 / 12 (3)

unde

b = lățime

h = înălțime

IY = b3 h / 12 (3b)

secțiune circulară solidă

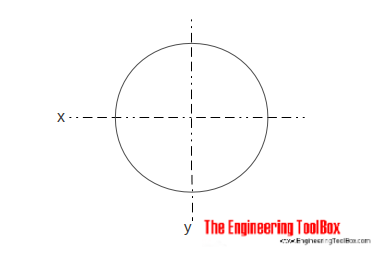
zona moment de inerție pentru o secțiune cilindrică solidă poate fi calculată ca

Ix = r4 /4

= D4 / 64 (4)

unde

r = raza

d = diametru

IY = R4 / 4

= D4 / 64 (4B)

secțiune cilindrică goală

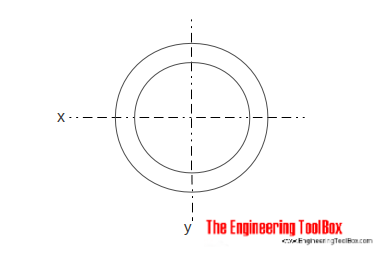
momentul de inerție pentru o secțiune cilindrică goală poate fi calculat ca

Ix = ) / 64 (5)

unde

do = diametrul exterior al cilindrului

di = diametrul interior al cilindrului

IY = secțiune pătrată (DO4 – di4) / 64 (5b)

– Momente diagonale

momentele diagonale de inerție pentru o secțiune pătrată pot fi calculate ca

Ix = Iy = a4 / 12 (6)

secțiunea dreptunghiulară-momentele zonei de pe orice linie prin Centrul de greutate

secțiunea dreptunghiulară și aria momentului de pe linia prin Centrul de greutate pot fi calculate ca

Ix = (b h / 12) (H2 cos2 A + B2 sin2 a) (7)

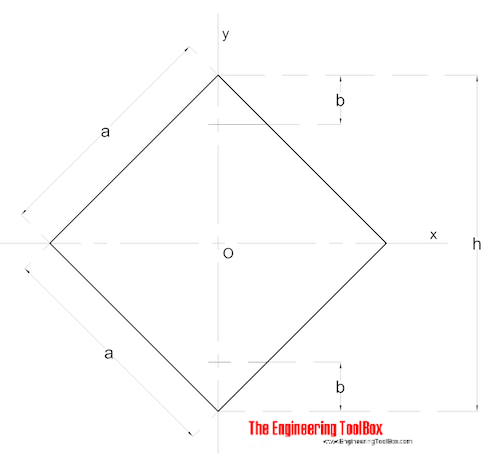
formă simetrică

zonă moment de inerție pentru o secțiunea în formă simetrică poate fi calculată ca

Ix = (a h3 / 12) + (b / 12) (H3-h3) (8)

Iy = (A3 h / 12) + (b3 / 12) (H – h) (8b)

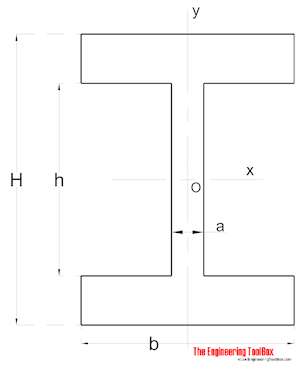
formă nesimetrică

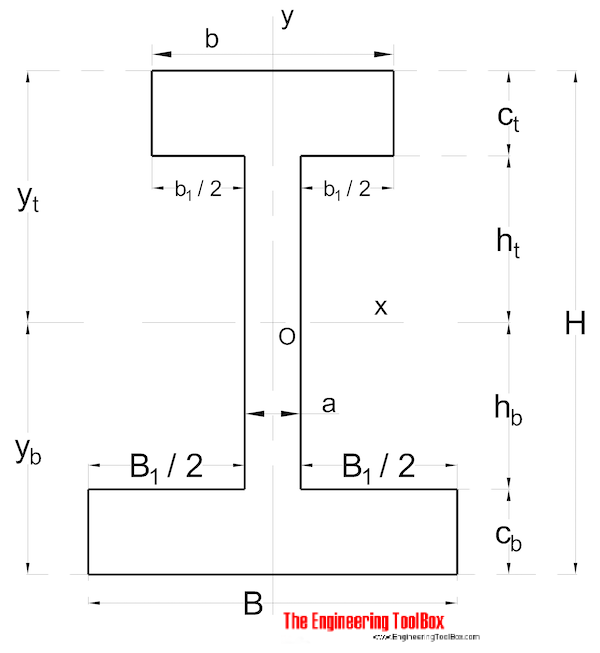
zonă moment de inerție pentru o secțiune nesimetrică poate fi calculată ca

Ix = (1 / 3) (B YB3 – B1 HB3 + b YT3 – B1 HT3) (9)

• zona momentul de inerție pentru secțiunile transversale tipice II

zona momentul de inerție vs. momentul Polar de inerție vs. Moment de inerție

• „momentul de inerție” este o proprietate de formă care este utilizată pentru a prezice deformarea, îndoirea și stresul în grinzi
• „momentul Polar de inerție” ca măsură a capacității unui fascicul de a rezista la torsiune – care este necesară pentru a calcula răsucirea unui fascicul supus cuplului
• „momentul de inerție” este o măsură a rezistenței unui obiect la schimbarea direcției de rotație.

modulul secțiunii

• „modulul secțiunii” este definit ca W = I / y, unde I este zona Moment de inerție și y este Distanța de la axa neutră la orice fibră dată