
















Timsort: velmi rychle , O(n log n), stabilní třídící algoritmus, postavený na reálném světě — nejsou vyrobeny v akademickém světě.
Klikněte zde chcete-li zobrazit aktualizovaný článek:

Timsort je třídící algoritmus, který je efektivní pro real-svět dat a není vytvořen v akademické laboratoři. Tim Peters vytvořil Timsort pro programovací jazyk Python v roce 2001. Timsort nejprve analyzuje seznam, který se snaží třídit, a poté zvolí přístup založený na analýze seznamu.
Protože algoritmus byl vynalezen byl použit jako výchozí třídění algoritmus v Python, Java, Android, a v GNU Octave.
Timsortova Velká o notace je O (n log n). Chcete-li se dozvědět o Big O notaci, přečtěte si toto.

Timsort je třídění čas je stejný jako Mergesort, který je rychlejší než většina ostatních druhů bys mohl vědět. Timsort ve skutečnosti využívá třídění Vložení a Mergesort, jak brzy uvidíte.
Peters navrhl Timsort používat již uspořádané prvky, které existují ve většině reálných datových sad. Tyto již uspořádané prvky nazývá „přirozenými běhy“. Iteruje přes data shromažďující prvky do běhů a současně slučuje tyto běhy dohromady do jednoho.
pole má v sobě méně než 64 prvků
pokud má pole, které se pokoušíme třídit, méně než 64 prvků, Timsort provede třídění vložení.
třídění vložení je jednoduchý druh, který je nejúčinnější na malých seznamech. Je to docela pomalé u větších seznamů, ale velmi rychle s malými seznamy. Myšlenka insertion sort je následující:
- Podívejte se na prvky jeden po druhém
- Vytvořit seřazený seznam vložením prvku na správné místo
Tady je stopa tabulka ukazuje, jak insertion sort by třídit seznam

V tomto případě jsme se vložení nově seřazené prvky do nové sub-pole, které začíná na začátku pole.
Tady je gif ukazuje, vložení sort:
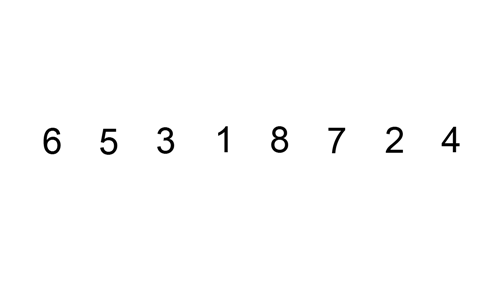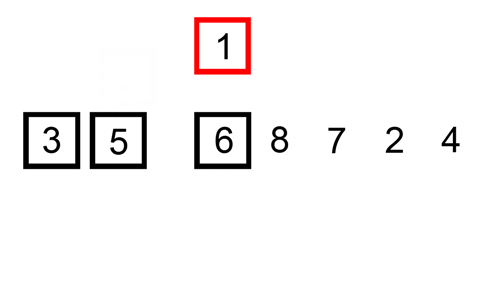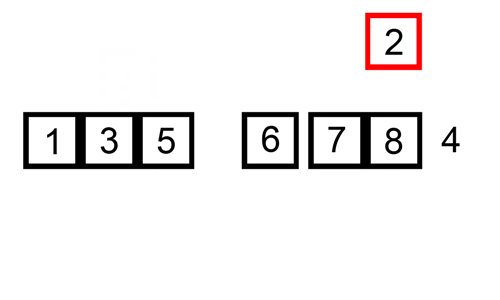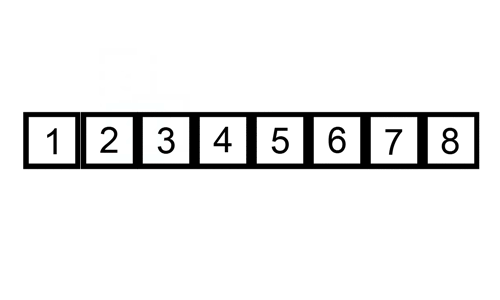
Více o běží
Pokud seznam je větší než 64 prvků než algoritmus bude nejprve projít seznam hledají pro díly, které jsou striktně rostoucí nebo klesající. Pokud část klesá, obrátí tuto část.
takže pokud běh klesá, bude to vypadat takto (kde běh je tučně):

pokud neklesne, bude to vypadat takto:

minrun je velikost, která je určena na základě velikosti pole. Algoritmus jej vybere tak, že většina běhů v náhodném poli má délku nebo se stane minrunem. Sloučení 2 polí je efektivnější, když je počet běhů roven nebo o něco menší než síla dvou. Timsort si vybere minrun, aby se pokusil zajistit tuto účinnost, tím, že se ujistí, že minrun je roven nebo menší než síla dvou.
algoritmus zvolí minrun z rozsahu 32 až 64 včetně. Zvolí minrun tak, že délka původního pole, pokud je vydělena minrunem, je rovna nebo o něco menší než síla dvou.
pokud je délka běhu menší než minrun, vypočítáte délku běhu od minrunu. Pomocí této nové číslo, chytit, že mnoho položek před spustit a provést vložení druh vytvořit nový běh.
takže pokud je minrun 63 A délka běhu je 33, uděláte 63-33 = 30. Poté uchopíte 30 prvků před koncem běhu, takže je to 30 položek z běhu a poté proveďte třídění vložení, abyste vytvořili nový běh.
po dokončení této části bychom nyní měli mít spoustu seřazených běhů v seznamu.
Sloučení

Timsort nyní provádí mergesort sloučit se spouští spolu. Nicméně, Timsort dbá na udržení stability a sloučit rovnováhu při sloučení třídění.
pro udržení stability bychom neměli vyměňovat 2 čísla stejné hodnoty. To nejen udržuje jejich původní pozice v seznamu, ale umožňuje algoritmus být rychlejší. Brzy budeme diskutovat o sloučení.
když Timsort najde běhy, přidá je do zásobníku. Jednoduchý zásobník by vypadal takto:

Představte si hromadu desek. Nemůžete vzít talíře zdola, takže je musíte vzít shora. Totéž platí o zásobníku.
Timsort se snaží vyvážit dvě konkurenční potřeby při spuštění mergesort. Na jedné straně bychom chtěli sloučení oddálit co nejdéle, abychom využili vzorce, které se mohou objevit později. Chtěli bychom však ještě více provést sloučení co nejdříve, abychom využili běh, který právě nalezený běh je stále vysoký v hierarchii paměti. Také nemůžeme odložit sloučení „příliš dlouho“, protože to spotřebovává paměť pamatovat běhy, které jsou stále unmerged, a zásobník má pevnou velikost.
ujistit Se, že máme tento kompromis, Timsort udržuje poslední tři položky na zásobníku a vytváří dva zákony, které musí platit tyto položky:
1. A > B + C
2. B > C
kde A, B A C jsou tři nejnovější položky na zásobníku.
slovy samotného Tima Peterse:
Co se ukázalo být dobrým kompromisem udržuje dva invarianty na stack položky, kde A, B a C jsou délky tří righmost ještě nejsou sloučeny plátky
Obvykle, sloučení přilehlých tratích různé délky v místě je těžké. Ještě těžší je, že musíme udržovat stabilitu. Chcete-li to obejít, Timsort vyhradí dočasnou paměť. Umístí menší (volání obou běhů a A B) ze dvou běhů do této dočasné paměti.
Cval

Zatímco Timsort je sloučení a a B, to si všimne, že jeden běh byl „vítězný“ mnohokrát za sebou. Pokud by se ukázalo, že běh a sestával ze zcela menších čísel než běh B, pak by běh a skončil zpět na svém původním místě. Sloučení obou běhů by vyžadovalo spoustu práce, aby se nic nedosáhlo.
více často než ne, data budou mít nějakou již existující vnitřní strukturu. Timsort předpokládá, že pokud hodně spustit hodnoty jsou nižší než B hodnoty, pak je pravděpodobné, že bude i nadále mít hodnoty menší než B.
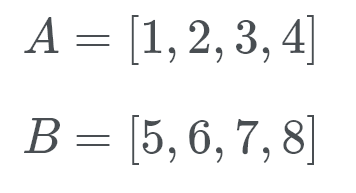
Timsort pak vstoupí do cválajícího režimu. Namísto kontroly a A B proti sobě provede Timsort binární vyhledávání vhodné polohy b V a. Timsort tak může přesunout celou část A na místo. Pak Timsort hledá vhodné umístění A v B. Timsort pak přesune celou část B plechovky najednou, a na místo.
podívejme se na to v akci. Timsort kontroly B (což je 5) a pomocí binární vyhledávací to vypadá na správném místě v A.
No, B patří na zadní seznamu A. Nyní Timsort kontroluje (což je 1) ve správné poloze. B. Tak jsme se podívat, kde číslo 1 pokračuje. Toto číslo je na začátku B. Nyní víme, že B patří na konci A A a patří na začátku B.
ukazuje se, že tato operace nestojí za to, pokud je vhodné místo pro B velmi blízko začátku A (nebo naopak). takže režim cvalu se rychle ukončí, pokud se nevyplácí. Timsort navíc bere na vědomí a ztěžuje pozdější vstup do režimu cvalu zvýšením počtu po sobě jdoucích výher pouze A nebo B, které jsou nutné pro vstup. Pokud se režim cval vyplácí, Timsort usnadňuje opětovné zadání.
Stručně řečeno, Timsort dělá 2 věci neuvěřitelně dobře:
- Skvělý výkon na pole s dříve existující vnitřní strukturu
- je schopen udržet stabilní druh
Dříve, za účelem dosažení stabilní druh, byste na zip položek ve vašem seznamu s celá čísla, a třídit je jako pole n-tice.
kód
pokud vás kód nezajímá, můžete tuto část přeskočit. Pod touto částí jsou další informace.
níže uvedený zdrojový kód je založen na práci mé a Nandy Javarmy. Zdrojový kód není úplný, ani není podobný oficiálnímu zdrojovému kódu Pythonu. Toto je jen hloupý Timsort, který jsem implementoval, abych získal obecný pocit Timsortu. Pokud chcete vidět původní zdrojový kód Timsort v celé své kráse, podívejte se na to zde. Timsort je oficiálně implementován v C, ne Python.
Timsort je ve skutečnosti postaven přímo do Pythonu, takže tento kód slouží pouze jako vysvětlovač. Chcete-li použít Timsort jednoduše napište:
list.sort()
Nebo
sorted(list)
Pokud se chcete naučit, jak Timsort funguje a získat pocit, pro to, vřele doporučuji zkusit realizovat sami!
tento článek je založen na původním úvodu Tim Peters do Timsortu, který najdete zde.