Angiv venligst tal adskilt af komma for at beregne.
relaterede statistikker Lommeregner / standardafvigelse Lommeregner / Stikprøvestørrelsesberegner
middel
ordet middelværdi, som er et homonym for flere andre ord på engelsk, er ligeledes tvetydigt, selv inden for matematik. Afhængigt af konteksten, hvad enten det er matematisk eller statistisk, hvad der menes med “Middel” ændringer. I sin enkleste matematiske definition vedrørende datasæt er det anvendte gennemsnit det aritmetiske gennemsnit, også kaldet matematisk forventning eller gennemsnit. I denne form henviser middelværdien til en mellemværdi mellem et diskret sæt tal, nemlig summen af alle værdier i datasættet divideret med det samlede antal værdier. Ligningen til beregning af et aritmetisk gennemsnit er næsten identisk med den til beregning af de statistiske begreber population og prøve gennemsnit, med små variationer i de anvendte variabler:
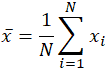
middelværdien betegnes ofte som H, udtales “H bar”, og selv i andre anvendelser, når variablen ikke er H, er stregnotationen en almindelig indikator for en eller anden form for middelværdi. I det specifikke tilfælde af befolkningsgennemsnit, snarere end at bruge variablen h, det græske symbol mu, eller L. A., bruges. På samme måde, eller snarere forvirrende, angives stikprøvegennemsnittet i statistikker ofte med et stort H. I betragtning af datasættet 10, 2, 38, 23, 38, 23, 21, anvendelse af summen ovenfor udbytter:
|
10 + 2 + 38 + 23 + 38 + 23 + 21
|
= | = 22.143 |
som tidligere nævnt er dette en af de enkleste definitioner af gennemsnittet, og nogle andre inkluderer det vægtede aritmetiske gennemsnit (som kun adskiller sig ved, at visse værdier i datasættet bidrager med mere værdi end andre) og geometrisk gennemsnit. Korrekt forståelse af givne situationer og sammenhænge kan ofte give en person de nødvendige værktøjer til at bestemme, hvilken statistisk relevant metode der skal bruges. Generelt, middelværdi, median, tilstand og rækkevidde bør ideelt set alle beregnes og analyseres for en given prøve eller datasæt, da de belyser forskellige aspekter af de givne data, og hvis de betragtes alene, kan føre til vildledning af dataene, som det vil blive demonstreret i de følgende afsnit.
Median
medianens statistiske koncept er en værdi, der deler en dataprøve, population eller sandsynlighedsfordeling i to halvdele. At finde medianen indebærer i det væsentlige at finde værdien i en dataprøve, der har en fysisk placering mellem resten af tallene. Bemærk, at når man beregner medianen for en endelig liste over tal, er rækkefølgen af dataprøverne vigtig. Konventionelt er værdierne angivet i stigende rækkefølge, men der er ingen reel grund til, at notering af værdierne i faldende rækkefølge ville give forskellige resultater. I det tilfælde, hvor det samlede antal værdier i en dataprøve er ulige, er medianen simpelthen tallet midt på listen over alle værdier. Når dataprøven indeholder et lige antal værdier, er medianen gennemsnittet af de to mellemværdier. Selvom dette kan være forvirrende, skal du blot huske, at selvom medianen undertiden involverer beregning af et gennemsnit, når dette tilfælde opstår, vil det kun involvere de to mellemværdier, mens et gennemsnit involverer alle værdierne i dataprøven. I de ulige tilfælde, hvor der kun er to dataprøver, eller der er et lige antal prøver, hvor alle værdierne er de samme, vil middelværdien og medianen være den samme. Givet det samme datasæt som før, medianen ville blive erhvervet på følgende måde:
2,10,21,23,23,38,38
efter at have noteret dataene i stigende rækkefølge og fastslået, at der er et ulige antal værdier, er det klart, at 23 er medianen givet denne sag. Hvis der var en anden værditilvækst til datasættet:
2,10,21,23,23,38,38,1027892
da der er et lige antal værdier, vil medianen være gennemsnittet af de to mellemtal, i dette tilfælde 23 og 23, Hvis gennemsnit er 23. Bemærk, at i dette særlige datasæt har tilføjelsen af en outlier (en værdi langt uden for det forventede værdiområde), værdien 1.027.892, ingen reel effekt på datasættet. Hvis gennemsnittet dog beregnes for dette datasæt, er resultatet 128.505, 875. Denne værdi er tydeligvis ikke en god repræsentation af de syv andre værdier i datasættet, der er langt mindre og tættere i værdi end gennemsnittet og outlier. Dette er den største fordel ved at bruge medianen til at beskrive statistiske data sammenlignet med gennemsnittet. Mens begge såvel som andre statistiske værdier skal beregnes, når der beskrives data, hvis kun en kan bruges, kan medianen give et bedre skøn over en typisk værdi i et givet datasæt, når der er ekstremt store variationer mellem værdier.
tilstand
i statistik er tilstanden den værdi i et datasæt, der har det højeste antal gentagelser. Det er muligt for et datasæt at være multimodalt, hvilket betyder, at det har mere end en tilstand. For eksempel:
2,10,21,23,23,38,38
både 23 og 38 vises to gange hver, hvilket gør dem begge til en tilstand for datasættet ovenfor.
på samme måde som middel og median bruges tilstanden som en måde at udtrykke information om tilfældige variabler og populationer. I modsætning til middel og median er tilstanden imidlertid et koncept, der kan anvendes på ikke-numeriske værdier såsom mærket af tortillachips, der oftest købes i en købmand. For eksempel, når man sammenligner mærkerne Tostitos, Mission og Tochitl, hvis det konstateres, at ved salg af tortillachips er tilstanden og sælger i et forhold på 3:2:1 sammenlignet med Tostitos og Mission brand tortillachips henholdsvis, kan forholdet bruges til at bestemme, hvor mange poser af hvert mærke der skal lagerføres. I det tilfælde, hvor 24 poser tortillachips sælges i en given periode, ville butikken lagre 12 poser med chips, 8 af Tostitos og 4 af Mission, hvis du bruger tilstanden. Hvis butikken simpelthen brugte et gennemsnit og solgte 8 poser af hver, kunne det potentielt miste 4 salg, hvis en kunde kun ønskede chips og ikke noget andet mærke. Som det fremgår af dette eksempel, er det vigtigt at tage alle manerer af statistiske værdier i betragtning, når man forsøger at drage konklusioner om en dataprøve.
rækkevidde
området for et datasæt i statistik er forskellen mellem de største og de mindste værdier. Mens rækkevidde har forskellige betydninger inden for forskellige områder af statistik og matematik, er dette dens mest grundlæggende definition, og det er det, der bruges af den medfølgende lommeregner. Brug det samme eksempel:
2,10,21,23,23,38,38
38 – 2 = 36
området i dette eksempel er 36. På samme måde som gennemsnittet kan området påvirkes væsentligt af ekstremt store eller små værdier. Samme eksempel som tidligere: