
















Timsort: en meget hurtig , o(n log n), stabil sorteringsalgoritme bygget til den virkelige verden — ikke konstrueret i den akademiske verden.
Klik her for at se den opdaterede artikel:

Timsort er en sorteringsalgoritme, der er effektiv til data i den virkelige verden og ikke oprettet i et akademisk laboratorium. Tim Peters oprettede Timsort til Python programmeringssprog i 2001. Timsort analyserer først den liste, den forsøger at sortere, og vælger derefter en tilgang baseret på analysen af listen.
siden algoritmen er opfundet, er den blevet brugt som standardsorteringsalgoritme i Python, Java, Android-platformen og i GNU Octave.
Timsorts store O-notation er O(n log n). For at lære om Big O notation, Læs dette.

Timsorts sorteringstid er den samme som Mergesort, hvilket er hurtigere end de fleste af de andre slags, du måske kender. Timsort faktisk gør brug af indsættelse sort og Mergesort, som du vil se snart.
Peters designet Timsort til at bruge allerede bestilte elementer, der findes i de fleste virkelige datasæt. Det kalder disse allerede bestilte elementer “naturlige kørsler”. Det gentager over de data, der indsamler elementerne i kørsler og samtidig fusionerer disse løber sammen til en.
arrayet har færre end 64 elementer i det
hvis det array, vi forsøger at sortere, har færre end 64 elementer i det, udfører Timsort en indsættelsessortering.
en indsætningssortering er en simpel sortering, der er mest effektiv på små lister. Det er ret langsomt på større lister, men meget hurtigt med små lister. Ideen om en indsættelsessortering er som følger:
- se på elementer en efter en
- Opbyg sorteret liste ved at indsætte elementet på det rigtige sted
her er en sporingstabel, der viser, hvordan indsætningssortering ville sortere listen

i dette tilfælde indsætter vi de nyligt sorterede elementer i et nyt underarray, der starter ved starten af arrayet.
her er en gif, der viser indsættelsessortering:
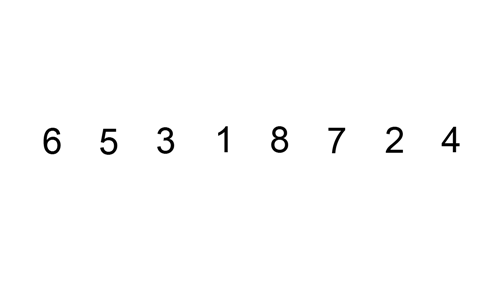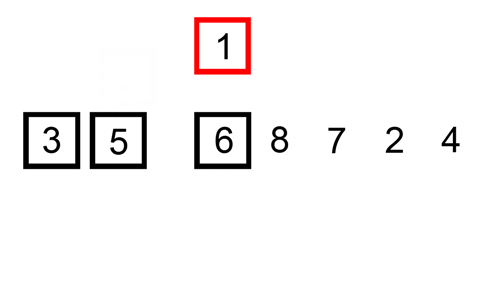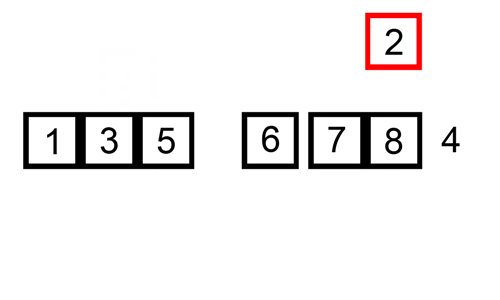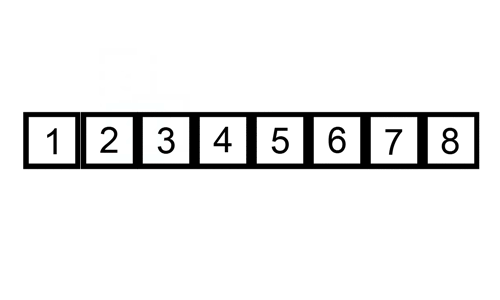
mere om kørsler
hvis listen er større end 64 elementer end algoritmen vil gøre en første passage gennem listen på udkig efter dele, der er strengt stigende eller faldende. Hvis delen falder, vil den vende den del.
så hvis løbet er faldende, vil det se sådan ud (hvor løbet er med fed skrift):

hvis ikke faldende, vil det se sådan ud:

minrun er en størrelse, der bestemmes ud fra størrelsen af arrayet. Algoritmen vælger den, så de fleste kørsler i et tilfældigt array er eller bliver minrun i længden. Sammenlægning af 2 arrays er mere effektiv, når antallet af kørsler er lig med eller lidt mindre end en effekt på to. Timsort vælger minrun for at forsøge at sikre denne effektivitet ved at sikre, at minrun er lig med eller mindre end en effekt på to.
algoritmen vælger minrun fra området 32 Til 64 inklusive. Det vælger minrun sådan, at længden af det oprindelige array, når divideret med minrun, er lig med eller lidt mindre end en effekt på to.
hvis længden af løbet er mindre end minrun, beregner du længden af det løb væk fra minrun. Ved hjælp af dette nye nummer griber du så mange elementer forud for løbet og udfører en indsætningssortering for at oprette et nyt løb.
så hvis minrun er 63 og længden af løbet er 33, gør du 63-33 = 30. Du griber derefter 30 elementer fra foran slutningen af løbet, så dette er 30 elementer fra løb og udfører derefter en indsætningssortering for at oprette et nyt løb.
når denne del er afsluttet, skal vi nu have en masse sorterede kørsler på en liste.
sammenlægning

Timsort udfører nu mergesort for at flette løbene sammen. Timsort sørger dog for at opretholde stabilitet og fusionere balance, mens fusionssortering.
for at opretholde stabilitet bør vi ikke udveksle 2 Tal af samme værdi. Dette holder ikke kun deres oprindelige positioner på listen, men gør det muligt for algoritmen at være hurtigere. Vi vil snart diskutere fusionsbalancen.
når Timsort finder kørsler, tilføjer det dem til en stak. En simpel stak ville se sådan ud:

Forestil dig en stak plader. Du kan ikke tage plader fra bunden, så du skal tage dem fra toppen. Det samme gælder for en stak.
Timsort forsøger at afbalancere to konkurrerende behov, når mergesort kører. På den ene side vil vi gerne udsætte fusionen så længe som muligt for at udnytte mønstre, der kan komme op senere. Men vi vil gerne have endnu mere at gøre sammenlægningen så hurtigt som muligt for at udnytte det løb, som det netop fundne løb stadig er højt i hukommelseshierarkiet. Vi kan heller ikke forsinke sammensmeltningen “for længe”, fordi den bruger hukommelse til at huske de kørsler, der stadig ikke er slået sammen, og stakken har en fast størrelse.
for at sikre, at vi har dette kompromis, holder Timsort styr på de tre seneste emner på stakken og opretter to love, der skal gælde for disse emner:
1. A > B + C
2. B > C
hvor A, B og C er de tre seneste elementer på stakken.
med ordene fra Tim Peters selv:
det, der viste sig at være et godt kompromis, opretholder to invarianter på stakindgange, hvor A, B og C er længderne af de tre højre ikke-endnu flettede skiver
normalt er det svært at flette tilstødende kørsler af forskellige længder på plads. Det, der gør det endnu sværere, er, at vi skal bevare stabiliteten. For at omgå dette sætter Timsort midlertidig hukommelse til side. Det placerer de mindre (kalder både kører A og B) af de to løber ind i den midlertidige hukommelse.
galopperende

mens Timsort fusionerer A og B, bemærker det, at et løb har “vundet” mange gange i træk. Hvis det viste sig, at løb a bestod af helt mindre tal end løb B, ville løb a ende tilbage på sit oprindelige sted. Sammenlægning af de to kørsler ville indebære en masse arbejde for at opnå noget.
oftere end ikke vil data have en allerede eksisterende intern struktur. Timsort antager, at hvis mange af run A ‘S værdier er lavere end run B’ S værdier, er det sandsynligt, at A fortsat vil have mindre værdier end B.
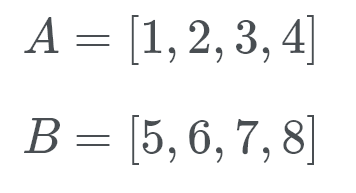
Timsort går derefter ind i galopperende tilstand. I stedet for at kontrollere A og B mod hinanden udfører Timsort en binær søgning efter den passende position af b I A. på denne måde kan Timsort flytte en hel del af A på plads. Derefter søger Timsort efter den passende placering af A I B. Timsort flytter derefter en hel del af B-dåse på en gang og på plads.
lad os se dette i aktion. Timsort kontrollerer B (som er 5), og ved hjælp af en binær søgning ser den efter den korrekte placering i A.
nå, B hører til på bagsiden af listen over A. nu kontrollerer Timsort For A (som er 1) på den rigtige placering af B. Så vi søger at se, hvor nummer 1 går. Dette nummer går i starten af B. Vi ved nu, at B hører hjemme i slutningen af A og A hører hjemme i starten af B.
det viser sig, at denne operation ikke er værd, hvis den passende placering for B er meget tæt på begyndelsen af A (eller omvendt). så galop mode afslutter hurtigt, hvis det ikke betaler sig. Derudover noterer Timsort sig og gør det sværere at gå ind i galoptilstand senere ved at øge antallet af på hinanden følgende a-Only-eller B-only-gevinster, der kræves for at komme ind. Hvis galoptilstand betaler sig, gør Timsort det lettere at indtaste igen.
kort sagt, Timsort gør 2 ting utroligt godt:
- stor ydeevne på arrays med allerede eksisterende intern struktur
- at være i stand til at opretholde en stabil sortering
tidligere, for at opnå en stabil sortering, ville du nødt til at lynlåse elementerne i din liste op med heltal, og sortere det som en vifte af tupler.
kode
hvis du ikke er interesseret i koden, er du velkommen til at springe denne del over. Der er nogle flere oplysninger under dette afsnit.
kildekoden nedenfor er baseret på mine og Nanda Javarmas arbejde. Kildekoden er ikke komplet, og den ligner heller ikke Pythons officielle sorterede() kildekode. Dette er bare en dumbed-ned Timsort jeg implementeret for at få en generel fornemmelse af Timsort. Hvis du vil se Timsorts originale kildekode i al sin herlighed, skal du tjekke den her. Timsort er officielt implementeret i C, ikke Python.
Timsort er faktisk bygget lige ind i Python, så denne kode fungerer kun som en forklarer. For at bruge Timsort skal du blot skrive:
list.sort()
eller
sorted(list)
hvis du vil mestre, hvordan Timsort fungerer og få en fornemmelse for det, foreslår jeg stærkt, at du prøver at implementere det selv!
denne artikel er baseret på Tim Peters’ oprindelige introduktion til Timsort, findes her.