Überlandfluss (oder Oberflächenabfluss) tritt in zwei Fällen auf:
1. wenn die Intensität des Niederschlags, der die Oberfläche erreicht, die Infiltrationskapazität des Bodens übersteigt. Dieser Prozess wird als Hortonian Overland Flow bezeichnet.
2. wenn die Kombination von Niederschlagsintensität und -dauer (und Abfluss aus höheren Gebieten) den Boden sättigt und den Grundwasserspiegel an die Oberfläche hebt. Dieser Prozess wird als Sättigung Überlandfluss bekannt.
Fallstudien: Niederlande; Belgien; Spanien; Kenia; Ghana, Kenia und Mali
Siehe auch:
- Senken
- Hortonische und Sättigungs-Überlandströmung (Infiltration)
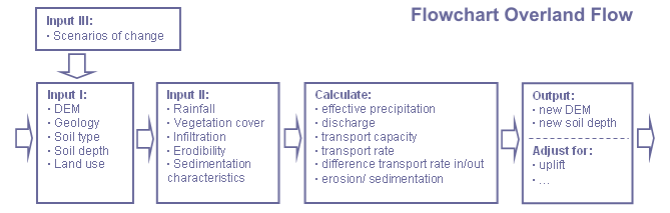
Technische Informationen
Das Modul Wassererosion und Sedimentation des Modells hat zwei grundlegende Annahmen: 1) Die potentielle Energie der Oberflächenwasserströmung ist die treibende Kraft für den Sedimenttransport und 2) Die Differenz zwischen Sedimenteintrag und -ausgang einer Gitterzelle ist gleich der Nettozunahme der Speicherung (Kontinuitätsgleichung für Sedimentbewegung) (Schoorl et al., 2000). Die Prozessbeschreibung stammt aus frühen Arbeiten von Kirkby (Kirkby, 1971) und Foster und Meyer (Foster und Meyer, 1972a; Foster und Meyer, 1972b), die 2D-Formeln verwenden, um Wassererosion und Sedimentation zu berechnen. Für das LAPSUS-Modell werden die Formeln angepasst, um räumliche (3D) Wassererosion und Sedimentation simulieren zu können (Schoorl et al., 2000). Die unten diskutierten Formeln basieren auf den 2D-Formeln von Kirkby und Foster und Meyer und mit den zugehörigen Einheiten (Foster und Meyer, 1972a; Foster und Meyer, 1972b; Kirkby, 1971).
Nach Berechnung des Abflusses Q kann die Sedimenttransportkapazität C (m2 Zeit-1) in der Gitterzelle als Funktion des Abflusses und der Steigung berechnet werden.:
(1.1) C = α * Qm · Λn
Wobei Λ der Steigungsgradient (∂z /∂x) (-) ist und m (-) und n (-) Konstanten sind, die einen Hinweis auf das untersuchte System geben: m = 0 und n = 1 deutet auf Bodenkriechen hin, während m = n = 3 auf große Flüsse hindeutet (Kirkby, 1971). Es können keine strengen Grenzen angegeben werden, da die Wirkung von m und n von Wechselwirkungen mit anderen Modellparametern abhängt. Dummy-Variable α wird verwendet, um die Einheiten zu korrigieren.
Die Sedimenttransportrate S (m2 Zeit-1) wird nach der integrierten Kontinuitätsgleichung für die Sedimentbewegung (Gl. 1.2 und 1.3). Die Zusammensetzung des in der Formel verwendeten E-Power-Terms hängt vom Gleichgewicht zwischen der Transportrate des bereits im Transport befindlichen Sediments S0 (m2-Zeit-1) (eingehende Sedimentflüsse aller höheren Nachbarn in der Gitterzelle) und der Sedimenttransportkapazität C ab: wenn S0 < C Erosion ergibt, während bei S0 > C Sedimentation resultiert. Wenn die Gitterzelle erodiert wird, wird die folgende Formel für die Sedimenttransportrate S verwendet:
(1.2) S = C + (S0 – C) · e -dx· D/C
Bei Ablagerung von Sedimenten in der Gitterzelle wird die folgende Formel für die Sedimenttransportrate S verwendet:
(1.3) S = C + (S0 – C)·e -dx·T/C
Wobei die Transportrate des Sediments S über die Gitterzellengröße dx(m) berechnet wird, indem die Sedimenttransportkapazität C mit der Transportrate des bereits im Transport befindlichen Sediments S0 (m2-Zeit-1) minus der Sedimenttransportkapazität C verglichen wird, reduziert um eine E-Leistung, die sich aus der Gitterzellengröße, der Ablösekapazität D oder der Absetzkapazität T und der Sedimenttransportkapazität C ergibt.
Die Ablösekapazität D (m Zeit-1), die darstellt, wie leicht Sediment von der Oberfläche erodiert wird, wird als Funktion des Abflusses und der Neigung berechnet.:
(1.4) D = Kes*Q*Λ
wobei Kes (m-1) ein zusammengefasster Oberflächenfaktor ist, der die Erodierbarkeit der Oberfläche anzeigt. Die Siedlungskapazität T (m time-1), die darstellt, wie leicht Sediment auf der Oberfläche abgelagert wird, wird wie folgt berechnet:
(1.5) D = Pes * Q* Λ
wobei Pes (m-1) ein Oberflächenfaktor ist, der die Eigenschaften der Klumpensedimentation angibt.
Durch Vergleich der Sedimenttransportrate S der Gitterzelle mit dem bereits transportierten Sediment S0 kann die Änderung der Sedimenttransportrate dS und damit Erosion oder Sedimentation berechnet werden.:
(1.6) dS = S – S0
dS kann auf Erosion oder Sedimentation in Metern umgerechnet werden, indem es durch die Gitterlänge dx (m) dividiert und mit dem Zeitschritt (time) multipliziert wird. Der resultierende Wert wird verwendet, um das digitale Höhenmodell und die Bodentiefenkarte für den folgenden Zeitschritt zu korrigieren.
Der Vergleich der E-Leistung bestimmt, wie viel von der Differenz zwischen Transportkapazität C und Transportrate des Sediments S in der Netzzelle „befriedigt“ werden kann. Abhängig von den Werten der beteiligten Variablen variiert die Resultierende der E-Leistung zwischen 0 und 1. In extremen Situationen, in denen dx und D / T zusammen viel größer als C sind, nähert sich die E-Leistung Null und die Transportrate des Sediments S ist gleich der Sedimenttransportkapazität C. Dann wird die maximale Erosion oder Sedimentation erreicht. Im anderen Extremfall, wenn dx und D / T kombiniert viel kleiner als C sind, nähert sich die E-Leistung 1 und die Transportrate von Sedimenten S ist gleich der Transportrate von Sedimenten, die sich bereits im Transport S0 befinden, und es tritt keine Erosion oder Ablagerung auf. In weniger extremen Situationen simuliert das Modell wahrscheinlich die Sedimenttransportrate S nahe der Transportkapazität C. Im Fall S0 > C wird mehr Sediment transportiert, als aufgrund der obigen Gitterzellen zulässig wäre, und es wird weniger als das maximale Sediment abgelagert. Die E-Power führt daher zu unter- und überkonzentrierten Strömungen im Modell, wodurch Erosion und Ablagerung über dem Hang geglättet werden. Offensichtlich ist das Ergebnis des E-Power-Vergleichs sehr einflussreich für Erosion und Sedimentation. Vergleich Eq. 1.1 und 1.4 / 1.5 Es ist klar, dass Entladung und Steigung sowohl an der Transportkapazität C als auch an den Berechnungen der Ablösekapazität D oder der Absetzkapazität T beteiligt sind. Da die Gitterzellengröße ein konstanter Wert ist, sind die Erodierbarkeit Kes und die Sedimentierbarkeit Pes die wichtigsten Variablen in einer Situation mit niedrigen m- und n-Werten. Wenn m und n größer sind, erhöht sich der Effekt der Transportkapazität C auf den E-Power-Term. Das Ergebnis des E-Power-Terms ist in dieser Situation schwieriger vorherzusagen.