Logarithmen: Einführung in „Die Beziehung“

Return to the Lessons Index | Do the Lessons in Order / Print-friendly page

Logarithmen: Einführung in
„Die Beziehung“ (Seite 1 von 3)

Abschnitte: Einführung in Protokolle, Vereinfachung von Protokollausdrücken, Allgemeine und natürliche Protokolle

Logarithmen sind das „Gegenteil“ von Exponentialen, so wie Subtraktion das Gegenteil von Addition und Division das Gegenteil von Multiplikation ist. Logs „Rückgängig“ Exponentiale. Technisch gesehen sind Logs die Inversen von Exponentialen.

In der Praxis fand ich es nützlich, an Protokolle in Bezug auf die Beziehung zu denken:

Links oben befindet sich die Exponentialaussage „y = bx“. Auf der rechten Seite oben ist „logb (y) = x“ die äquivalente logarithmische Aussage, die ausgesprochen wird „log-base-b von y ist gleich x“; Der Wert des subskribierten „b“ ist „die Basis des Logarithmus“, genau wie b die Basis im Exponentialausdruck „bx“ ist. Und so wie die Basis b in einem Exponential immer positiv und ungleich 1 ist, so ist auch die Basis b für einen Logarithmus immer positiv und ungleich 1. Was auch immer sich im Logarithmus befindet, wird als „Argument“ des Protokolls bezeichnet. Beachten Sie, dass die Basis sowohl in der Exponentialgleichung als auch in der logarithmischen Gleichung (oben) „b“ ist, dass x und y jedoch die Seiten wechseln, wenn Sie zwischen den beiden Gleichungen wechseln.

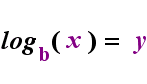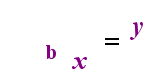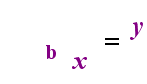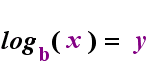
Wenn Sie sich an diese Beziehung erinnern können (was auch immer das Argument des Logars war, wird zum „Gleichen“ und was auch immer das „Gleiche“ war, wird zum Exponenten im Exponential und umgekehrt), dann sollten Sie nicht zu viel haben Probleme mit Logarithmen.

(Ich habe den Begriff „Die Beziehung“ selbst geprägt. Sie werden es nicht in Ihrem Text finden, und Ihre Lehrer und Tutoren werden keine Ahnung haben, wovon Sie sprechen, wenn Sie es ihnen gegenüber erwähnen. „Die Beziehung“ ist eine völlig nicht standardisierte Terminologie. Warum benutze ich es trotzdem? Weil es funktioniert.)

Übrigens: Wenn Sie bemerkt haben, dass ich die Variablen zwischen den beiden Feldern mit der Anzeige „Die Beziehung“ gewechselt habe, haben Sie ein scharfes Auge. Ich habe das absichtlich getan, um zu betonen, dass es nicht um die Variablen selbst geht, sondern darum, wie sie sich bewegen.

• Konvertieren Sie „63 = 216“ in den entsprechenden logarithmischen Ausdruck.

Zum Konvertieren bleibt die Basis (dh die 6)gleich, aber die 3 und die 216 wechseln die Seiten. Das gibt mir:

log6(216) = 3 Copyright © Elizabeth Stapel 2002-2011 Alle Rechte vorbehalten

• Konvertieren Sie „log4 (1024) = 5“ in den entsprechenden Exponentialausdruck.

Zum Konvertieren bleibt die Basis (dh die 4) gleich, aber die 1024 und die 5 wechseln die Seiten. Das gibt mir:

45 = 1024

Oben | 1 | 2 | 3 | Zurück zum Index Weiter >>