Bitte geben Sie zur Berechnung kommagetrennte Zahlen an.
Verwandte Statistiken Rechner / Standardabweichungsrechner / Stichprobengrößenrechner
Mittelwert
Das Wort Mittelwert, das ein Homonym für mehrere andere Wörter in der englischen Sprache ist, ist selbst im Bereich der Mathematik ähnlich zweideutig. Je nach Kontext, ob mathematisch oder statistisch, ändert sich, was mit dem „Mittelwert“ gemeint ist. In seiner einfachsten mathematischen Definition in Bezug auf Datensätze wird als Mittelwert das arithmetische Mittel verwendet, das auch als mathematische Erwartung oder Durchschnitt bezeichnet wird. In dieser Form bezieht sich der Mittelwert auf einen Zwischenwert zwischen einem diskreten Satz von Zahlen, nämlich die Summe aller Werte in dem Datensatz, geteilt durch die Gesamtzahl der Werte. Die Gleichung zur Berechnung eines arithmetischen Mittels ist praktisch identisch mit der zur Berechnung der statistischen Konzepte von Grundgesamtheit und Stichprobenmittelwert, mit geringfügigen Abweichungen in den verwendeten Variablen:
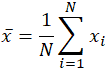
Der Mittelwert wird oft als x bezeichnet, ausgesprochen „x bar“, und selbst in anderen Verwendungen, wenn die Variable nicht x ist, ist die Balkennotation ein häufiger Indikator für irgendeine Form von Mittelwert. Im speziellen Fall des Mittelwerts der Grundgesamtheit wird anstelle der Variablen x das griechische Symbol mu oder μ verwendet. Ähnlich oder eher verwirrend wird der Stichprobenmittelwert in der Statistik oft mit einem Großbuchstaben X angegeben. Angesichts des Datensatzes 10, 2, 38, 23, 38, 23, 21, die Anwendung der obigen Summation ergibt:
|
10 + 2 + 38 + 23 + 38 + 23 + 21
|
= | = 22.143 |
Wie bereits erwähnt, ist dies eine der einfachsten Definitionen des Mittelwerts, und einige andere umfassen das gewichtete arithmetische Mittel (das sich nur dadurch unterscheidet, dass bestimmte Werte im Datensatz mehr Wert beisteuern als andere) und das geometrische Mittel. Das richtige Verständnis bestimmter Situationen und Kontexte kann einer Person oft die Werkzeuge zur Verfügung stellen, die erforderlich sind, um zu bestimmen, welche statistisch relevante Methode verwendet werden soll. Im Allgemeinen sollten Mittelwert, Median, Modus und Bereich idealerweise alle für eine bestimmte Stichprobe oder einen Datensatz berechnet und analysiert werden, da sie verschiedene Aspekte der gegebenen Daten erläutern und, wenn sie allein betrachtet werden, zu falschen Darstellungen der Daten führen können, wie in den folgenden Abschnitten gezeigt wird.
Median
Das statistische Konzept des Medians ist ein Wert, der eine Datenstichprobe, Population oder Wahrscheinlichkeitsverteilung in zwei Hälften teilt. Das Ermitteln des Medians umfasst im Wesentlichen das Ermitteln des Werts in einer Datenstichprobe, die eine physische Position zwischen den übrigen Zahlen aufweist. Beachten Sie, dass bei der Berechnung des Medians einer endlichen Liste von Zahlen die Reihenfolge der Datenstichproben wichtig ist. Herkömmlicherweise werden die Werte in aufsteigender Reihenfolge aufgelistet, aber es gibt keinen wirklichen Grund, warum das Auflisten der Werte in absteigender Reihenfolge zu unterschiedlichen Ergebnissen führen würde. Wenn die Gesamtzahl der Werte in einer Datenstichprobe ungerade ist, ist der Median einfach die Zahl in der Mitte der Liste aller Werte. Wenn die Datenstichprobe eine gerade Anzahl von Werten enthält, ist der Median der Mittelwert der beiden mittleren Werte. Obwohl dies verwirrend sein kann, denken Sie einfach daran, dass der Median, obwohl er manchmal die Berechnung eines Mittelwerts beinhaltet, in diesem Fall nur die beiden mittleren Werte umfasst, während ein Mittelwert alle Werte in der Datenstichprobe umfasst. In den ungeraden Fällen, in denen es nur zwei Datenstichproben gibt oder in denen es eine gerade Anzahl von Stichproben gibt, in denen alle Werte gleich sind, sind Mittelwert und Median gleich. Bei gleichem Datensatz wie zuvor würde der Median auf folgende Weise erfasst:
2,10,21,23,23,38,38
Nachdem die Daten in aufsteigender Reihenfolge aufgelistet und festgestellt wurden, dass es eine ungerade Anzahl von Werten gibt, ist klar, dass 23 in diesem Fall der Median ist. Wenn dem Datensatz ein weiterer Mehrwert hinzugefügt würde:
2,10,21,23,23,38,38,1027892
Da es eine gerade Anzahl von Werten gibt, ist der Median der Durchschnitt der beiden mittleren Zahlen, in diesem Fall 23 und 23, deren Mittelwert 23 ist. Beachten Sie, dass in diesem speziellen Datensatz das Hinzufügen eines Ausreißers (ein Wert, der weit außerhalb des erwarteten Wertebereichs liegt), des Werts 1.027.892, keine wirkliche Auswirkung auf den Datensatz hat. Wenn jedoch der Mittelwert für diesen Datensatz berechnet wird, ist das Ergebnis 128.505,875. Dieser Wert ist eindeutig keine gute Darstellung der sieben anderen Werte im Datensatz, die viel kleiner und näher am Wert als der Durchschnitt und der Ausreißer sind. Dies ist der Hauptvorteil der Verwendung des Medians bei der Beschreibung statistischer Daten im Vergleich zum Mittelwert. Während beide und andere statistische Werte bei der Beschreibung von Daten berechnet werden sollten, kann der Median, wenn nur einer verwendet werden kann, eine bessere Schätzung eines typischen Werts in einem bestimmten Datensatz liefern, wenn extrem große Abweichungen zwischen den Werten vorliegen.
Modus
In Statistiken ist der Modus der Wert in einem Datensatz mit der höchsten Anzahl von Wiederholungen. Es ist möglich, dass ein Datensatz multimodal ist, was bedeutet, dass er mehr als einen Modus hat. Zum Beispiel:
2,10,21,23,23,38,38
Sowohl 23 als auch 38 erscheinen jeweils zweimal, was sie beide zu einem Modus für den obigen Datensatz macht.
Ähnlich wie Mittelwert und Median wird der Modus verwendet, um Informationen über Zufallsvariablen und Populationen auszudrücken. Im Gegensatz zu Mittelwert und Median ist der Modus jedoch ein Konzept, das auf nicht numerische Werte wie die Marke der Tortilla-Chips angewendet werden kann, die am häufigsten in einem Lebensmittelgeschäft gekauft werden. Wenn beispielsweise beim Vergleich der Marken Tostitos, Mission und XOCHiTL festgestellt wird, dass beim Verkauf von Tortillachips XOCHiTL der Modus ist und im Verhältnis 3: 2: 1 im Vergleich zu Tortillachips der Marken Tostitos und Mission verkauft, kann das Verhältnis verwendet werden, um zu bestimmen, wie viele Beutel jeder Marke auf Lager sind. In dem Fall, in dem 24 Säcke Tortillachips während eines bestimmten Zeitraums verkauft werden, würde das Geschäft 12 Säcke XOCHiTL-Chips, 8 Tostitos und 4 Mission auf Lager haben, wenn der Modus verwendet wird. Wenn das Geschäft jedoch nur einen Durchschnitt verwendete und jeweils 8 Beutel verkaufte, könnte es möglicherweise 4 Verkäufe verlieren, wenn ein Kunde nur XOCHiTL-Chips und keine andere Marke wünschte. Wie aus diesem Beispiel hervorgeht, ist es wichtig, alle Arten von statistischen Werten zu berücksichtigen, wenn versucht wird, Rückschlüsse auf eine Datenstichprobe zu ziehen.
Bereich
Der Bereich eines Datensatzes in der Statistik ist die Differenz zwischen dem größten und dem kleinsten Wert. Während der Bereich in verschiedenen Bereichen der Statistik und Mathematik unterschiedliche Bedeutungen hat, ist dies die grundlegendste Definition und wird vom bereitgestellten Taschenrechner verwendet. Verwenden des gleichen Beispiels:
2,10,21,23,23,38,38
38 – 2 = 36
Der Bereich in diesem Beispiel ist 36. Ähnlich wie der Mittelwert kann der Bereich durch extrem große oder kleine Werte erheblich beeinflusst werden. Verwenden Sie das gleiche Beispiel wie zuvor: