
















Timsort: Ein sehr schneller, O (n log n), stabiler Sortieralgorithmus für die reale Welt — nicht in der Wissenschaft konstruiert.
Klicken Sie hier, um den aktualisierten Artikel anzuzeigen:

Timsort ist ein Sortieralgorithmus, der für reale Daten effizient ist und nicht in einem akademischen Labor erstellt wurde. Tim Peters schuf Timsort für die Programmiersprache Python im Jahr 2001. Timsort analysiert zuerst die Liste, die es zu sortieren versucht, und wählt dann einen Ansatz basierend auf der Analyse der Liste.
Seit der Erfindung des Algorithmus wurde er als Standard-Sortieralgorithmus in Python, Java, der Android-Plattform und in GNU Octave verwendet.
Timsorts große O-Notation ist O(n log n). Um mehr über die Big O-Notation zu erfahren, lesen Sie dies.

Die Sortierzeit von Timsort entspricht der von Mergesort , die schneller ist als die meisten anderen Sortierungen, die Sie möglicherweise kennen. Timsort verwendet tatsächlich Insertion sort und Mergesort , wie Sie bald sehen werden.
Peters entwarf Timsort, um bereits geordnete Elemente zu verwenden, die in den meisten realen Datensätzen vorhanden sind. Es nennt diese bereits geordneten Elemente „natürliche Läufe“. Es iteriert über die Daten, die die Elemente zu Läufen sammeln und diese Läufe gleichzeitig zu einem zusammenführen.
Das Array enthält weniger als 64 Elemente
Wenn das Array, das wir sortieren möchten, weniger als 64 Elemente enthält, führt Timsort eine Einfügesortierung aus.
Eine Einfügesortierung ist eine einfache Sortierung, die bei kleinen Listen am effektivsten ist. Es ist ziemlich langsam bei größeren Listen, aber sehr schnell mit kleinen Listen. Die Idee einer Einfügesortierung lautet wie folgt:
- Sehen Sie sich die Elemente einzeln an
- Erstellen Sie eine sortierte Liste, indem Sie das Element an der richtigen Stelle einfügen
Hier ist eine Ablaufverfolgungstabelle, die zeigt, wie die Einfügesortierung die Liste sortieren würde

In diesem Fall fügen wir die neu sortierten Elemente in ein neues Unterarray ein, das am Anfang des Arrays beginnt.
Hier ist ein GIF, das Einfügesortierung zeigt:
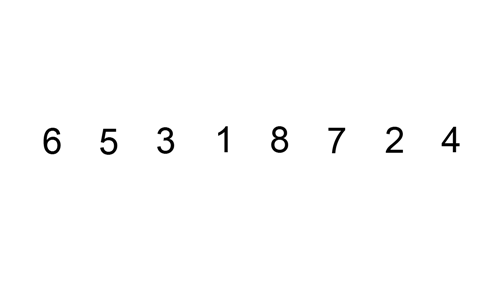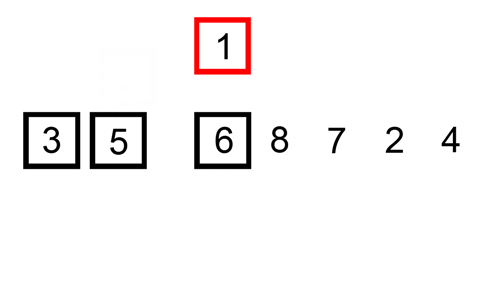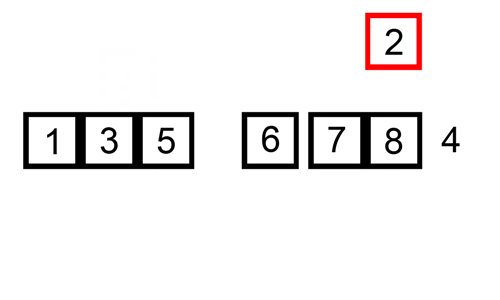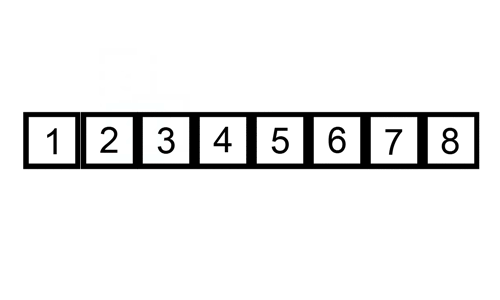
Mehr über Läufe
Wenn die Liste größer als 64 Elemente ist, führt der Algorithmus einen ersten Durchgang durch die Liste durch und sucht nach Teilen, die streng zunehmen oder abnehmen. Wenn der Teil abnimmt, wird dieser Teil umgekehrt.
Wenn der Lauf also abnimmt, sieht er folgendermaßen aus (wobei der Lauf fett gedruckt ist):

Wenn nicht verringert, wird es so aussehen:

Die minimale Größe ist eine Größe, die basierend auf der Größe des Arrays bestimmt wird. Der Algorithmus wählt es so aus, dass die meisten Läufe in einem zufälligen Array minrun sind oder minrun werden. Das Zusammenführen von 2 Arrays ist effizienter, wenn die Anzahl der Läufe gleich oder geringfügig kleiner als eine Potenz von zwei ist. Timsort wählt minrun, um diese Effizienz sicherzustellen, indem sichergestellt wird, dass minrun gleich oder kleiner als eine Potenz von zwei ist.
Der Algorithmus wählt minrun aus dem Bereich 32 bis einschließlich 64. Es wählt minrun so aus, dass die Länge des ursprünglichen Arrays, wenn sie durch minrun geteilt wird, gleich oder geringfügig kleiner als eine Potenz von zwei ist.
Wenn die Länge des Laufs kleiner als minrun ist, berechnen Sie die Länge dieses Laufs weg von minrun. Mit dieser neuen Nummer greifen Sie so viele Elemente vor dem Lauf und führen eine Einfügesortierung durch, um einen neuen Lauf zu erstellen.
Wenn also minrun 63 und die Länge des Laufs 33 beträgt, machen Sie 63-33 = 30. Sie greifen dann auf 30 Elemente vor dem Ende des Laufs zu, also auf 30 Elemente aus dem Lauf, und führen dann eine Einfügesortierung durch, um einen neuen Lauf zu erstellen.
Nachdem dieser Teil abgeschlossen ist, sollten wir nun eine Reihe sortierter Läufe in einer Liste haben.
Zusammenführen

Timsort führt jetzt Mergesort aus, um die Läufe zusammenzuführen. Timsort stellt jedoch sicher, dass die Stabilität und das Zusammenführungsgleichgewicht beim Zusammenführen der Sortierung erhalten bleiben.
Um die Stabilität zu erhalten, sollten wir 2 Zahlen mit gleichem Wert nicht austauschen. Dadurch bleiben nicht nur die ursprünglichen Positionen in der Liste erhalten, sondern der Algorithmus kann auch schneller sein. Wir werden in Kürze die Merge-Balance diskutieren.
Wenn Timsort runs findet, werden sie einem Stapel hinzugefügt. Ein einfacher Stapel würde so aussehen:

Stellen Sie sich einen Stapel Platten vor. Sie können keine Teller von unten nehmen, also müssen Sie sie von oben nehmen. Das gleiche gilt für einen Stapel.
Timsort versucht, zwei konkurrierende Anforderungen auszugleichen, wenn mergesort ausgeführt wird. Einerseits möchten wir das Zusammenführen so lange wie möglich verzögern, um später auftretende Muster auszunutzen. Aber wir möchten noch mehr, um die Zusammenführung so schnell wie möglich durchzuführen, um den Lauf auszunutzen, dass der gerade gefundene Lauf immer noch hoch in der Speicherhierarchie ist. Wir können das Zusammenführen auch nicht „zu lange“ verzögern, da es Speicher verbraucht, um sich an die Läufe zu erinnern, die noch nicht zusammengeführt wurden, und der Stapel eine feste Größe hat.
Um sicherzustellen, dass wir diesen Kompromiss haben, verfolgt Timsort die drei neuesten Elemente auf dem Stapel und erstellt zwei Gesetze, die für diese Elemente gelten müssen:
1. EIN > B + C
2. B > C
Wobei A, B und C die drei letzten Elemente auf dem Stapel sind.
In den Worten von Tim Peters selbst:
Was sich als guter Kompromiss herausstellte, behält zwei Invarianten auf den Stapeleinträgen bei, wobei A, B und C die Längen der drei rechtesten noch nicht zusammengeführten Slices sind
Normalerweise ist das Zusammenführen benachbarter Läufe unterschiedlicher Länge schwierig. Was es noch schwieriger macht, ist, dass wir Stabilität bewahren müssen. Um dies zu umgehen, Timsort beiseite temporären Speicher. Es platziert den kleineren (Aufruf beider Läufe A und B) der beiden Läufe in diesen temporären Speicher.
Galoppierend

Während Timsort A und B zusammenführt, wird festgestellt, dass ein Lauf viele Male hintereinander „gewonnen“ hat. Wenn sich herausstellte, dass der Lauf A aus völlig kleineren Zahlen bestand als der Lauf B, würde der Lauf A wieder an seinem ursprünglichen Platz landen. Das Zusammenführen der beiden Läufe würde viel Arbeit bedeuten, um nichts zu erreichen.
In den meisten Fällen haben Daten eine bereits vorhandene interne Struktur. Timsort geht davon aus, dass, wenn viele Werte von Run A niedriger als die Werte von Run B sind, es wahrscheinlich ist, dass A weiterhin kleinere Werte als B hat.
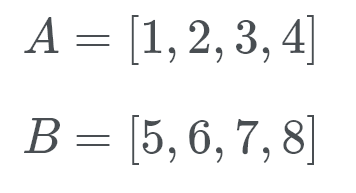
Timsort wechselt dann in den galoppierenden Modus. Anstatt A und B gegeneinander zu überprüfen, führt Timsort eine binäre Suche nach der entsprechenden Position von b in a durch. Timsort sucht dann nach der entsprechenden Position von A in B. Timsort verschiebt dann einen ganzen Abschnitt von B auf einmal und an seinen Platz.
Sehen wir uns das in Aktion an. Timsort prüft B (das ist 5) und sucht mit einer binären Suche nach der richtigen Stelle in A.
Nun, B gehört ganz hinten in die Liste von A. Jetzt sucht Timsort nach A (das ist 1) an der richtigen Stelle von B. Wir wollen also sehen, wohin die Nummer 1 geht. Wir wissen jetzt, dass B am Ende von A und A am Anfang von B gehört.
Es stellt sich heraus, dass sich diese Operation nicht lohnt, wenn der geeignete Ort für B sehr nahe am Anfang von A liegt (oder umgekehrt). der Galopp-Modus wird also schnell beendet, wenn er sich nicht auszahlt. Darüber hinaus nimmt Timsort zur Kenntnis und erschwert den späteren Einstieg in den Galopp-Modus, indem die Anzahl der aufeinanderfolgenden A-Only- oder B-Only-Siege erhöht wird, die für die Teilnahme erforderlich sind. Wenn sich der Galopp-Modus auszahlt, erleichtert Timsort den erneuten Einstieg.
Kurz gesagt, Timsort macht 2 Dinge unglaublich gut:
- Hervorragende Leistung bei Arrays mit bereits vorhandener interner Struktur
- In der Lage sein, eine stabile Sortierung aufrechtzuerhalten
Um eine stabile Sortierung zu erreichen, müssten Sie die Elemente in Ihrer Liste mit Ganzzahlen komprimieren und als Array von Tupeln sortieren.
Code
Wenn Sie nicht an dem Code interessiert sind, können Sie diesen Teil überspringen. Unter diesem Abschnitt finden Sie weitere Informationen.
Der folgende Quellcode basiert auf meiner und Nanda Javarmas Arbeit. Der Quellcode ist weder vollständig noch ähnelt er dem offiziellen sorted() -Quellcode von Python. Dies ist nur ein verdummter Timsort, den ich implementiert habe, um ein allgemeines Gefühl für Timsort zu bekommen. Wenn Sie den ursprünglichen Quellcode von Timsort in seiner ganzen Pracht sehen möchten, schauen Sie es sich hier an. Timsort ist offiziell in C implementiert, nicht in Python.
Timsort ist tatsächlich direkt in Python integriert, daher dient dieser Code nur als Erklärung. Um Timsort zu verwenden, schreiben Sie einfach:
list.sort()
Oder
sorted(list)
Wenn Sie die Funktionsweise von Timsort beherrschen und ein Gefühl dafür bekommen möchten, empfehle ich Ihnen dringend, es selbst zu implementieren!
Dieser Artikel basiert auf Tim Peters ‚ursprünglicher Einführung in Timsort, die Sie hier finden.