jos meidän tavoitteena on löytää relativistic yleistys Poisson ’ s yhtälö gravitaatiokentän:
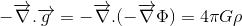
missä Φ viittaa gravitaatiopotentiaaliin ja ρ massatiheyteen, olemme puolivälissä.
näimme jo edellisessä artikkelissamme energian ja liikemäärän tensorin, että massatiheyden yleistys (yhtälön oikeanpuoleinen termi) vastaa energian ja liikemäärän Tµv: tä.
on siis järkevää olettaa, että yhtälömme tulisi olla muotoa:
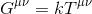
missä k tarkoittaa skalaaria ja Gµv, niin kutsuttu Einsteinin tensori edustaa aika-avaruuden kaarevuutta kuvaavaa sijoitus-2 tensoria .
sikäli kuin tiedämme, Gµv: n tulisi noudattaa seuraavia rajoitteita:
– sen pitäisi mitätöidä tasaisessa aika – avaruudessa
– sen pitäisi kuvata aika – avaruuden kaarevuutta ja olla lineaarinen Riemannin tensorin suhteen
– sen pitäisi olla symmetrinen ja sijalla 2 (tµv: nä)
-sillä pitäisi olla nollaeroja (tµv: na)
-ja lopuksi Newtonin raja-arvot, sen pitäisi pienentyä 4ngp: hen
ensimmäisellä yrityksellä Ricci tensorin ollessa ratkaisuna
muistamme artikkelistamme Newtonin rajan geodeettisen yhtälön, että gravitaatiopotentiaali φ liittyy metriikan 00-komponenttiin via H00=(G00-1)/C2
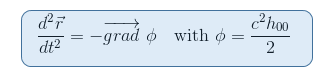
se näyttää sitten luonnollista etsiä tensori, johon liittyy toinen derivaatat, metriikka, joka on tapauksessa Riemannin tensori. Lisäksi Riemannin tensori on toistaiseksi ainoa ehdokas, jonka tiedämme pystyvän kuvaamaan aika-avaruuden kaarevuutta (vrt.toinen rajoitus edellä).
koska meidän on löydettävä sijoitus-2 tensori, ja jos oletamme, että meidän on löydettävä ratkaisu yksinomaan Riemannin tensorin kannalta, on luonnollista tarkastella ensin Riemannin tensorin supistunutta muotoa, joka tunnetaan nimellä Riccin tensori.
tämän nähdäksemme muistakaamme Riemannin tensorin lauseke artikkelista Riemannin kaarevuustensori osa II: derivointi geodeettisesta poikkeamasta
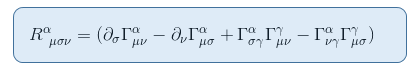
staattisen ja heikon gravitaatiokentän rajassa vain yksi termi vaikuttaa R00: aan:
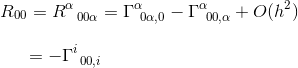
samassa artikkelissa, olemme laskeneet tämän Christoffel symboli ja totesi, että
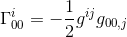
kun likiarvo Gij = nij ja goo, j = hoo, j (katso artikkeli) saamme:
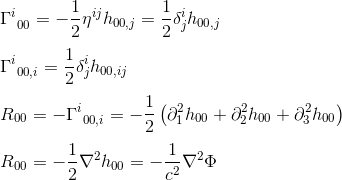
R00: n tunnistaminen ΔΦ: llä (Laplacian operaattori) viittaa siihen, että yleisen suhteellisuusteorian kenttäyhtälön tulisi rinnastaa Rab: n Vakiokertoimeen Sarkaimella.
vuonna 1915 Einstein pystyi tämän yhtälön avulla jopa ratkaisemaan Merkuriuksen perihelin prekession pitkäaikaisen ongelman, mikä sai kirjoittamaan saman vuoden marraskuussa, että ”muutaman päivän ajan olin vieressäni iloisen innostuksen vallassa.”
lopulta Einstein joutui hylkäämään tämän ensimmäisen yrityksen, koska yleensä Rab: n divergenssi ei mitätöi.
toinen yritys
on tensori, joka liittyy läheisesti Riccin skalaariin wihch voidaan asettaa ristiriidatta vasemmalle puolelle. Näin saadaan Einsteinin tensori määriteltyä seuraavasti:
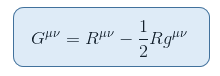
missä R = Raa on Riccin skalaari tai skalaarin kaarevuus.
tämä Gabin muoto on symmetrinen ja sijoitus-2 ja kuvaa selvästi aika-avaruuden kaarevuutta. Joten se vain jää osoittamaan, että koko derivaatta on nolla
tehdäksemme tämän, aloitamme Bianchin identiteetillä
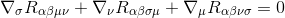
kertomalla kautta gγσgαμgβν (metriikan derivaatat ovat nolla, joten ne toimivat vakioina ja voidaan ottaa johdannaisten sisälle), saadaan:
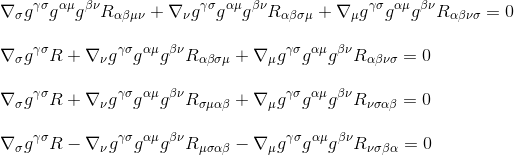
käyttämällä Riccin tensorimääritelmää Rµv=gμβgνσRβσ (Vaihe 3) ja nimeämällä indeksit uudelleen (VAIHE 4) saadaan
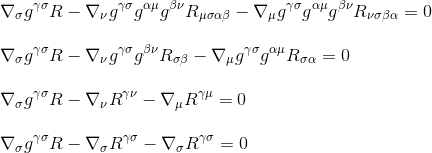
factorising johdannainen, saamme vihdoin
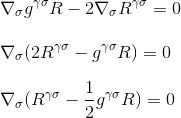
mikä on juuri sitä, mitä halusimme osoittaa: ero Einstein tensor on nolla, ja olemme löytäneet oikean ehdokkaan vasemmalla puolella meidän kaarevuus/massa-energia yhtälö.