Logarithmes : Introduction à « La Relation »

Retour à l’Index des leçons | Faites les leçons dans l’ordre / Page facile à imprimer

Logarithmes: Introduction à
« La Relation » (page 1 sur 3)

Sections: Introduction aux logs, Simplification des expressions de logs, logs communs et naturels

Les logarithmes sont le « contraire » des exponentielles, tout comme la soustraction est le contraire de l’addition et la division est le contraire de la multiplication. Enregistre les exponentielles « annulées ». Techniquement parlant, les logs sont les inverses des exponentielles.

En termes pratiques, j’ai trouvé utile de penser aux logs en termes de Relation:

Sur le côté gauche ci-dessus se trouve l’instruction exponentielle « y = bx ». Sur le côté droit ci-dessus, « logb(y) = x » est l’instruction logarithmique équivalente, qui se prononce « log-base-b de y est égal à x »; La valeur de l’indice « b » est « la base du logarithme », tout comme b est la base de l’expression exponentielle « bx ». Et, de même que la base b dans une exponentielle est toujours positive et non égale à 1, de même la base b pour un logarithme est toujours positive et non égale à 1. Tout ce qui se trouve à l’intérieur du logarithme est appelé « argument » du journal. Notez que la base de l’équation exponentielle et de l’équation log (ci-dessus) est « b », mais que les x et y changent de côté lorsque vous basculez entre les deux équations.

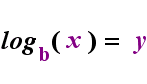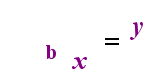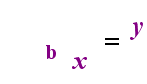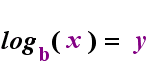
Si vous pouvez vous souvenir de cette relation (que tout ce qui avait été l’argument du journal devient les « égaux » et tout ce qui avait été les « égaux » devient l’exposant dans l’exponentielle, et vice versa), alors vous ne devriez pas avoir trop de problèmes avec les logarithmes.

(J’ai moi-même inventé le terme « Relation ». Vous ne le trouverez pas dans votre texte, et vos enseignants et tuteurs n’auront aucune idée de ce dont vous parlez si vous leur en parlez. « La relation » est une terminologie totalement non standard. Pourquoi je l’utilise quand même? Parce que ça marche.)

Au fait: Si vous avez remarqué que j’ai commuté les variables entre les deux cases affichant « La Relation », vous avez un œil aiguisé. Je l’ai fait exprès, pour souligner que le point n’est pas les variables elles-mêmes, mais comment elles se déplacent.

• Convertissez « 63 = 216 » en l’expression logarithmique équivalente.

Pour convertir, la base (c’est-à-dire le 6) reste la même, mais le 3 et le 216 commutent de côté. Cela me donne:

log6 (216) =3 Copyright © Elizabeth Stapel 2002-2011 Tous droits réservés

• Convertissez « log4(1024) = 5 » en l’expression exponentielle équivalente.

Pour convertir, la base (c’est-à-dire le 4) reste la même, mais le 1024 et le 5 commutent les côtés. Cela me donne:

45 = 1024

Haut | 1 | 2 | 3 | Retour à l’index Suivant >>