
















Timsort: Un algorithme de tri très rapide, O (n log n) et stable construit pour le monde réel – pas construit dans le milieu universitaire.
Cliquez ici pour voir l’article mis à jour:

Timsort est un algorithme de tri efficace pour les données du monde réel et non créé dans un laboratoire académique. Tim Peters a créé Timsort pour le langage de programmation Python en 2001. Timsort analyse d’abord la liste qu’il essaie de trier, puis choisit une approche basée sur l’analyse de la liste.
Depuis que l’algorithme a été inventé, il a été utilisé comme algorithme de tri par défaut en Python, Java, la plate-forme Android et dans GNU Octave.
La notation du grand O de Timsort est O(n log n). Pour en savoir plus sur la notation Big O, lisez ceci.

Le temps de tri de Timsort est le même que celui de Mergesort, qui est plus rapide que la plupart des autres types que vous connaissez peut-être. Timsort utilise en fait le tri par insertion et le Mergesort, comme vous le verrez bientôt.
Peters a conçu Timsort pour utiliser des éléments déjà commandés qui existent dans la plupart des ensembles de données du monde réel. Il appelle ces éléments déjà ordonnés des « courses naturelles ». Il itère les données collectant les éléments en exécutions et fusionne simultanément ces exécutions en une seule.
Le tableau contient moins de 64 éléments
Si le tableau que nous essayons de trier contient moins de 64 éléments, Timsort exécutera un tri par insertion.
Un tri par insertion est un tri simple qui est le plus efficace sur les petites listes. C’est assez lent pour les listes plus grandes, mais très rapide avec les petites listes. L’idée d’un tri par insertion est la suivante:
- Regardez les éléments un par un
- Créez une liste triée en insérant l’élément à l’emplacement correct
Voici un tableau de traces montrant comment le tri par insertion trierait la liste

Dans ce cas, nous insérons les éléments nouvellement triés dans un nouveau sous-tableau, qui commence au début du tableau.
Voici un gif montrant le tri par insertion:
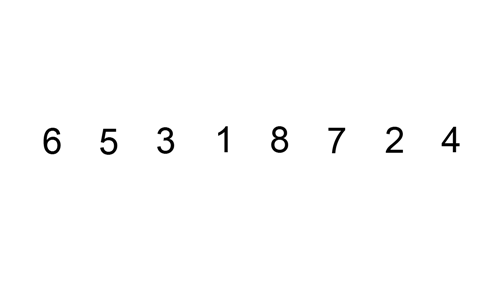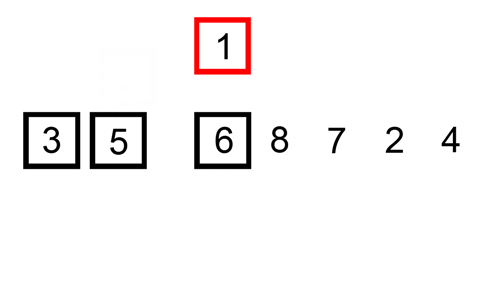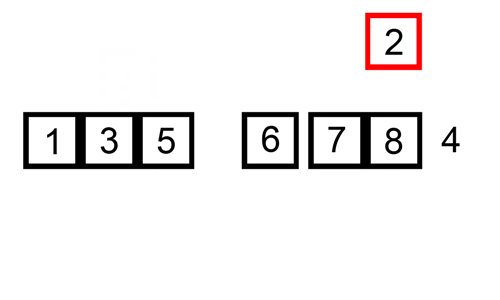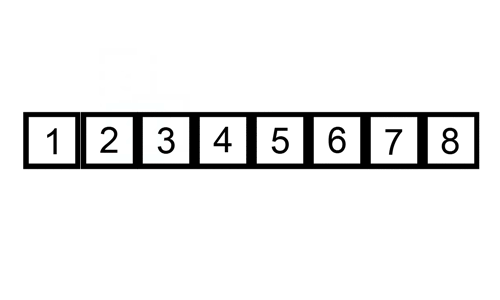
En savoir plus sur les exécutions
Si la liste est supérieure à 64 éléments, l’algorithme effectuera un premier passage dans la liste à la recherche de parties qui augmentent ou diminuent strictement. Si la partie diminue, elle inversera cette partie.
Donc, si la course diminue, cela ressemblera à ceci (où la course est en gras):

Si elle ne diminue pas, cela ressemblera à ceci:

Le minrun est une taille déterminée en fonction de la taille du tableau. L’algorithme le sélectionne de sorte que la plupart des exécutions d’un tableau aléatoire soient, ou deviennent minrun, en longueur. La fusion de 2 tableaux est plus efficace lorsque le nombre d’exécutions est égal ou légèrement inférieur à une puissance de deux. Timsort choisit minrun pour essayer d’assurer cette efficacité, en s’assurant que minrun est égal ou inférieur à une puissance de deux.
L’algorithme choisit minrun dans la plage de 32 à 64 inclus. Il choisit minrun de telle sorte que la longueur du tableau d’origine, lorsqu’elle est divisée par minrun, soit égale ou légèrement inférieure à une puissance de deux.
Si la longueur de la course est inférieure à minrun, vous calculez la longueur de cette course à partir de minrun. En utilisant ce nouveau nombre, vous récupérez autant d’éléments avant l’exécution et effectuez un tri par insertion pour créer une nouvelle exécution.
Donc, si minrun est 63 et que la longueur de la course est 33, vous faites 63-33 = 30. Vous récupérez ensuite 30 éléments devant la fin de l’exécution, il s’agit donc de 30 éléments de l’exécution, puis effectuez un tri par insertion pour créer une nouvelle exécution.
Une fois cette partie terminée, nous devrions maintenant avoir un tas d’exécutions triées dans une liste.
Fusion

Timsort effectue maintenant le mergesort pour fusionner les exécutions ensemble. Cependant, Timsort veille à maintenir la stabilité et l’équilibre de fusion lors du tri de fusion.
Pour maintenir la stabilité, nous ne devons pas échanger 2 nombres de valeur égale. Cela permet non seulement de conserver leurs positions d’origine dans la liste, mais permet également à l’algorithme d’être plus rapide. Nous discuterons sous peu du solde de la fusion.
Lorsque Timsort trouve des exécutions, il les ajoute à une pile. Une pile simple ressemblerait à ceci:

Imaginez une pile de plaques. Vous ne pouvez pas prendre les assiettes par le bas, vous devez donc les prendre par le haut. La même chose est vraie à propos d’une pile.
Timsort essaie d’équilibrer deux besoins concurrents lors de l’exécution de mergesort. D’une part, nous aimerions retarder la fusion le plus longtemps possible afin d’exploiter des modèles qui pourraient apparaître plus tard. Mais nous aimerions encore plus faire la fusion le plus tôt possible pour exploiter la course que la course vient de trouver est encore élevée dans la hiérarchie de la mémoire. Nous ne pouvons pas non plus retarder la fusion « trop longtemps » car elle consomme de la mémoire pour se souvenir des exécutions qui ne sont toujours pas fusionnées, et la pile a une taille fixe.
Pour être sûr d’avoir ce compromis, Timsort garde une trace des trois éléments les plus récents de la pile et crée deux lois qui doivent s’appliquer à ces éléments :
1. A > B + C
2. B > C
Où A, B et C sont les trois éléments les plus récents de la pile.
Selon les mots de Tim Peters lui-même:
Ce qui s’est avéré être un bon compromis maintient deux invariants sur les entrées de pile, où A, B et C sont les longueurs des trois tranches les plus à droite non encore fusionnées
Habituellement, il est difficile de fusionner des séries adjacentes de différentes longueurs en place. Ce qui rend les choses encore plus difficiles, c’est que nous devons maintenir la stabilité. Pour contourner cela, Timsort met de côté la mémoire temporaire. Il place le plus petit (appelant les deux runs A et B) des deux runs dans cette mémoire temporaire.
Au galop

Alors que Timsort fusionne A et B, il remarque qu’une course a « gagné » plusieurs fois de suite. S’il s’avérait que la course A se composait de nombres entièrement plus petits que la course B, la course A se retrouverait à sa place d’origine. Fusionner les deux pistes impliquerait beaucoup de travail pour ne rien réaliser.
Le plus souvent, les données auront une structure interne préexistante. Timsort suppose que si de nombreuses valeurs de l’exécution A sont inférieures aux valeurs de l’exécution B, il est probable que A continuera d’avoir des valeurs plus petites que B.
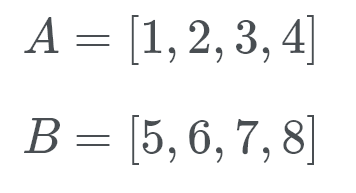
Timsort passe alors en mode galop. Au lieu de vérifier A et B l’un par rapport à l’autre, Timsort effectue une recherche binaire pour la position appropriée de b dans a. De cette façon, Timsort peut déplacer une section entière de A en place. Ensuite, Timsort recherche l’emplacement approprié de A dans B. Timsort déplacera alors une section entière de B peut à la fois, et en place.
Voyons cela en action. Timsort vérifie B (qui est 5) et en utilisant une recherche binaire, il recherche l’emplacement correct dans A.
Eh bien, B appartient à la fin de la liste de A. Maintenant, Timsort vérifie A (qui est 1) à l’emplacement correct de B. Nous cherchons donc à voir où va le nombre 1. Ce nombre va au début de B. Nous savons maintenant que B appartient à la fin de A et A appartient au début de B.
Il s’avère que cette opération n’en vaut pas la peine si l’emplacement approprié pour B est très proche du début de A (ou vice versa). le mode galop se termine donc rapidement s’il ne porte pas ses fruits. De plus, Timsort prend note et rend plus difficile l’entrée en mode galop plus tard en augmentant le nombre de victoires consécutives A uniquement ou B uniquement requises pour entrer. Si le mode galop porte ses fruits, Timsort facilite la rentrée.
En bref, Timsort fait 2 choses incroyablement bien:
- Excellentes performances sur les tableaux avec une structure interne préexistante
- Pouvoir maintenir un tri stable
Auparavant, pour obtenir un tri stable, vous deviez compresser les éléments de votre liste avec des entiers et les trier comme un tableau de tuples.
Code
Si le code ne vous intéresse pas, n’hésitez pas à ignorer cette partie. Il y a plus d’informations ci-dessous cette section.
Le code source ci-dessous est basé sur le travail du mien et de Nanda Javarma. Le code source n’est pas complet, ni similaire au code source officiel de Python tried(). C’est juste un Timsort stupide que j’ai implémenté pour avoir une idée générale de Timsort. Si vous voulez voir le code source original de Timsort dans toute sa splendeur, vérifiez-le ici. Timsort est officiellement implémenté en C, pas en Python.
Timsort est en fait directement intégré à Python, ce code ne sert donc qu’à expliquer. Pour utiliser Timsort, il suffit d’écrire:
list.sort()
Ou
sorted(list)
Si vous voulez maîtriser le fonctionnement de Timsort et en avoir une idée, je vous suggère fortement d’essayer de l’implémenter vous-même!
Cet article est basé sur l’introduction originale de Tim Peters à Timsort, trouvée ici.