unde este o funcție la un punct înalt sau scăzut? Calculul poate ajuta!
un maxim este un punct înalt și un minim este un punct scăzut:
într-o funcție cu schimbare lină, un maxim sau un minim este întotdeauna locul în care funcția se aplatizează (cu excepția unui punct de șa).
unde se aplatizează? Unde panta este zero.
unde este panta zero? Derivatul ne spune!
să ne scufundăm cu un exemplu:

- exemplu: o minge este aruncată în aer. Înălțimea sa în orice moment t este dată de:
- care este înălțimea sa maximă?
- o reîmprospătare rapidă a derivatelor
- cum știm că este un maxim (sau minim)?
- al doilea test derivat
- exemplu: găsiți maximele și minimele pentru:
- cuvinte
- încă un exemplu
- exemplu: găsiți maximele și minimele pentru:
- trebuie să fie diferențiat
- exemplu: Ce zici de funcția f(x) = |x| (valoare absolută) ?
exemplu: o minge este aruncată în aer. Înălțimea sa în orice moment t este dată de:
h = 3 + 14t − 5t2
care este înălțimea sa maximă?
folosind derivate putem găsi panta acestei funcții:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
(Vezi mai jos acest exemplu pentru modul în care am găsit acea derivată.)

acum Găsiți când panta este zero:
panta este zero la t = 1,4 secunde
și înălțimea la acel moment este:
și astfel:
înălțimea maximă este de 12,8 m (la t = 1,4 s)
o reîmprospătare rapidă a derivatelor
un derivat găsește practic panta unei funcții.
în exemplul anterior am luat acest lucru:
h = 3 + 14T-5t2
și a venit cu acest derivat:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
care ne spune panta funcției în orice moment T
am folosit aceste reguli derivate:
- panta unei valori constante (ca 3) este 0
- panta unei linii ca 2x este 2, deci 14t are o pantă de 14
- o funcție pătrată ca t2 are o pantă de 2t, deci 5t2 are o pantă de 5 (2t)
- și apoi le-am adăugat: 0 + 14 − 5 (2t)
cum știm că este un maxim (sau minim)?
am văzut-o pe grafic! Dar altfel … derivații vin din nou la salvare.
luați derivata pantei (a doua derivată a funcției originale):
derivata 14-10t este -10
aceasta înseamnă că panta devine continuu mai mică (-10): călătorind de la stânga la dreapta panta începe pozitiv (funcția crește), trece prin zero (punctul plat), iar apoi panta devine negativă (funcția scade):

o pantă care devine mai mică (și merge deși 0) înseamnă un maxim.
aceasta se numește al doilea test derivat
pe graficul de mai sus am arătat panta înainte și după, dar în practică facem testul în punctul în care panta este zero:
al doilea test derivat
când panta unei funcții este zero la x, iar a doua derivată la x este:
- mai puțin de 0, este un maxim local
- mai mare de 0, este un minim local
- egal cu 0, atunci testul eșuează (pot exista și alte modalități de a afla, deși)
„al doilea derivat: mai puțin de 0 este un maxim, mai mare de 0 este un minim”
exemplu: găsiți maximele și minimele pentru:
y = 5×3 + 2×2 – 3x
derivata (panta) este:
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
care este pătratic cu zerouri la:
- x = -3/5
- x = +1/3
ar putea fi maxime sau minime? (Nu te uita încă la Grafic!)
a doua derivată este y” = 30x + 4
la x = -3/5:
la x = +1/3:
(acum puteți privi graficul.)
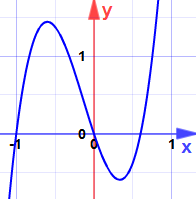
cuvinte
un punct înalt se numește Maxim (plural maxime).
un punct scăzut se numește minim (plural minime).
cuvântul general pentru maxim sau minim este extremum (plural extrema).
spunem maxim local (sau minim) atunci când pot exista puncte mai mari (sau mai mici) în altă parte, dar nu în apropiere.
încă un exemplu
exemplu: găsiți maximele și minimele pentru:
y = x3-6×2 + 12x-5
derivata este:
![]() y = 3×2-12x + 12
y = 3×2-12x + 12
care este pătratic cu un singur zero la x = 2
este un maxim sau minim?
a doua derivată este y” = 6x − 12
la x = 2:
și iată de ce:
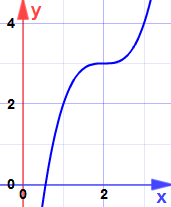
este un punct de șa … panta devine zero, dar nu este nici maximă, nici minimă.
trebuie să fie diferențiat
și există un punct tehnic important:
funcția trebuie să fie diferențiată (derivata trebuie să existe în fiecare punct din domeniul său).
exemplu: Ce zici de funcția f(x) = |x| (valoare absolută) ?
| |x / arată astfel: |  |
la x = 0 are o schimbare foarte ascuțită!
de fapt, nu este diferențiat acolo (așa cum se arată pe pagina diferențiabilă).
deci nu putem folosi această metodă pentru funcția valoare absolută.
funcția trebuie să fie, de asemenea, continuă, dar orice funcție diferențiată este, de asemenea, continuă, deci nu trebuie să vă faceți griji în legătură cu asta.

