hvor er en funktion på et højt eller lavt punkt? Calculus kan hjælpe!
et maksimum er et højt punkt og et minimum er et lavt punkt:

i en funktion, der skifter jævnt, er der altid et maksimum eller minimum, hvor funktionen flader ud (undtagen et sadelpunkt).
hvor flader det ud? Hvor hældningen er nul.
hvor er hældningen nul? Derivatet fortæller os!
lad os dykke lige ind med et eksempel:

- eksempel: en bold kastes i luften. Dens højde til enhver tid t er givet af:
- Hvad er dens maksimale højde?
- en hurtig genopfriskning på derivater
- Hvordan ved vi, at det er et maksimum (eller Minimum)?
- anden Derivattest
- eksempel: find maksima og minima for:
- ord
- endnu et eksempel
- eksempel: find maksima og minima for:
- skal være differentierbar
- eksempel: hvad med funktionen f(H) = |H| (absolut værdi) ?
eksempel: en bold kastes i luften. Dens højde til enhver tid t er givet af:
h = 3 + 14T − 5t2
Hvad er dens maksimale højde?
ved hjælp af derivater kan vi finde hældningen af denne funktion:
![]() h = 0 + 14 − 5(2T)
h = 0 + 14 − 5(2T)
= 14 − 10t
(se nedenfor dette eksempel for, hvordan vi fandt det afledte.)

find nu, når hældningen er nul:
hældningen er nul ved t = 1,4 sekunder
og højden på det tidspunkt er:
og så:
den maksimale højde er 12,8 m (ved t = 1,4 s)
en hurtig genopfriskning på derivater
et derivat finder dybest set hældningen af en funktion.
i det foregående eksempel tog vi dette:
h = 3 + 14T-5t2
og kom op med dette derivat:
![]() h = 0 + 14 − 5 (2T)
h = 0 + 14 − 5 (2T)
= 14 − 10T
som fortæller os hældningen af funktionen til enhver tid t
vi brugte disse afledte regler:
- hældningen af en konstant værdi (som 3) er 0
- hældningen af en linje som 2H er 2, så 14t har en hældning på 14
- en firkantet funktion som t2 har en hældning på 2T, så 5t2 har en hældning på 5 (2T)
- og så tilføjede vi dem: 0 + 14 − 5 (2t)
Hvordan ved vi, at det er et maksimum (eller Minimum)?
vi så det på grafen! Men ellers … derivater kommer til undsætning igen.
Tag derivatet af hældningen (det andet derivat af den oprindelige funktion):
derivatet af 14 − 10T er -10
dette betyder, at hældningen konstant bliver mindre (-10): at rejse fra venstre mod højre skråningen starter positivt (funktionen stiger), går gennem nul (det flade punkt), og derefter bliver hældningen negativ (funktionen falder):

en hældning, der bliver mindre (og går dog 0) betyder et maksimum.
dette kaldes den anden afledte Test
på grafen ovenfor viste jeg hældningen før og efter, men i praksis udfører vi testen på det punkt, hvor hældningen er nul:
anden Derivattest
når en funktions hældning er nul ved:
- mindre end 0, Det er et lokalt maksimum
- større end 0, Det er et lokalt minimum
- lig med 0, så fejler testen (der kan være andre måder at finde ud af om)
“andet derivat: mindre end 0 er et maksimum, større end 0 er et minimum”
eksempel: find maksima og minima for:
y = 5H3 + 2H2 – 3h
derivatet (hældning) er:
![]() y = 15h2 + 4 gange− 3
y = 15h2 + 4 gange− 3
hvilket er kvadratisk med nuller på:
- e = -3/5
- k = +1/3
kan det være Maksima eller minima? (Se ikke på grafen endnu!)
det andet derivat er y” = 30 gange + 4
at = -3/5:
ved = +1/3:
(nu kan du se på grafen.)
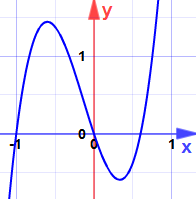
ord
et højdepunkt kaldes et maksimum (flertal Maksima).
et lavpunkt kaldes et minimum (flertal minima).
det generelle ord for maksimum eller minimum er ekstremum (flertal ekstrema).
vi siger lokalt maksimum (eller minimum), når der kan være højere (eller lavere) point andre steder, men ikke i nærheden.
endnu et eksempel
eksempel: find maksima og minima for:
y = 3 − 6H2 + 12h − 5
derivatet er:
![]() y = 3H2 − 12h + 12
y = 3H2 − 12h + 12
hvilket er kvadratisk med kun et nul ved 2
er det et maksimum eller minimum?
det andet derivat er y” = 6 gange-12
at = 2:
og her er hvorfor:
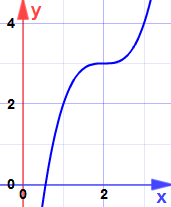
det er et sadelpunkt … hældningen bliver nul, men det er hverken et maksimum eller minimum.
skal være differentierbar
og der er et vigtigt teknisk punkt:
funktionen skal være differentierbar (derivatet skal eksistere på hvert punkt i sit domæne).
eksempel: hvad med funktionen f(H) = |H| (absolut værdi) ?
| |ser sådan ud: |  |
ved H=0 har det en meget spids ændring!
faktisk er det ikke differentierbart der (som vist på den differentierbare side).
så vi kan ikke bruge denne metode til funktionen absolut værdi.
funktionen skal også være kontinuerlig, men enhver funktion, der kan differentieres, er også kontinuerlig, så ingen grund til at bekymre sig om det.
