a biteltolódásokat néha bitenkénti műveleteknek tekintik, mert az értéket bitek sorozataként kezelik, nem pedig numerikus mennyiségként. Ezekben a műveletekben a számjegyeket balra vagy jobbra mozgatják vagy eltolják. A számítógépes processzorban lévő regiszterek rögzített szélességűek, így egyes bitek az egyik végén “eltolódnak” a regiszterből, míg ugyanannyi bit “tolódik be” a másik végből; a biteltolás operátorai közötti különbségek abban rejlenek, hogy hogyan határozzák meg az eltolt bitek értékeit.
Bit addressingEdit
ha a regiszter szélessége (gyakran 32 vagy akár 64) nagyobb, mint a legkisebb címezhető egység (atomi elem) bitjeinek száma (általában 8), amelyet gyakran bájtnak hívnak, a shift műveletek címzési sémát indukálnak a biteken.Figyelmen kívül hagyva a határhatásokat a regiszter mindkét végén, az aritmetikai és logikai eltolási műveletek ugyanúgy viselkednek, és a 8 bites pozícióval történő eltolás a bitmintát 1 bájtos pozícióval szállítja a következő módon:
|
a bal oldali eltolás 8 pozícióval növeli a byte címet 1 |
|
a 8 pozícióval történő jobb eltolás csökkenti a byte címet 1 |
|
a bal oldali eltolás 8 pozícióval csökkenti a byte címet 1 |
|
a 8 pozícióval történő jobb eltolás növeli a byte címet 1 |
aritmetikai váltásszerkesztés

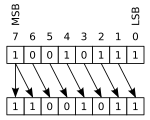
aritmetikai eltolódás esetén a két végből eltolt biteket eldobják. Bal aritmetikai eltolásban a nullák jobbra tolódnak; jobb aritmetikai eltolódásban a jelbit (a MSB kettes komplementerében) balra tolódik, így megőrizve az operandus előjelét.
ez a példa egy 8 bites regisztert használ, amelyet kettő kiegészítéseként értelmeznek:
00010111 (decimal +23) LEFT-SHIFT= 00101110 (decimal +46)
10010111 (decimal −105) RIGHT-SHIFT= 11001011 (decimal −53)
az első esetben a bal szélső számjegy eltolódott a regiszter vége mellett, az új 0 pedig a jobb szélső helyzetbe került. A második esetben a jobb szélső 1-et eltolták (talán a carry flag-be), az új 1-et pedig a bal szélső helyzetbe másolták, megőrizve a szám előjelét. A több műszakot néha néhány számjeggyel egyetlen műszakra rövidítik. Például:
00010111 (decimal +23) LEFT-SHIFT-BY-TWO= 01011100 (decimal +92)
a bal aritmetikai eltolás n – vel egyenértékű a 2-vel való szorzással n (feltéve, hogy az érték nem túlcsordul), míg a jobb aritmetikai eltolás n-vel a kettő KOMPLEMENT értéke megegyezik a 2-vel való osztással n és kerekítés felé negatív végtelen. Ha a bináris számot egyesek komplementereként kezeljük, akkor ugyanaz a jobbra tolási művelet 2N-vel osztást és nulla felé kerekítést eredményez.
logikai váltásszerkesztés
 bal logikai váltás
|
 jobb logikai váltás
|
logikai eltolódás esetén a nullák be vannak tolva az eldobott bitek cseréjéhez. Ezért a logikai és aritmetikai bal eltolódások pontosan ugyanazok.
mivel azonban a logikai jobb shift 0 bitet szúr be a legjelentősebb bitbe, a jelbit másolása helyett ideális az aláíratlan bináris számokhoz, míg az aritmetikai jobb shift ideális az aláírt kettő komplementer bináris számaihoz.
Circular shiftEdit
a shift másik formája a circular shift, bitenkénti forgatás vagy bitforgatás.
Forgatásszerkesztés
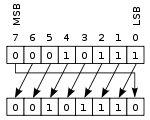 bal kör alakú eltolás vagy forgatás
|
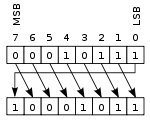 jobb körkörös eltolás vagy forgatás
|
ebben a műveletben, amelyet néha rotate no carry-nek hívnak, a biteket úgy “forgatják”, mintha a regiszter bal és jobb vége összekapcsolódna. A bal oldali eltolás során jobbra eltolt érték az az érték, amelyet balra toltak el, és fordítva egy jobb oldali eltolás esetén. Ez akkor hasznos, ha meg kell őrizni az összes meglévő bitet, és gyakran használják a digitális kriptográfiában.
forgassa át a hordozótszerkesztés
 balra forgassa át a hordozást
|
 jobbra forgassa át a hordozást
|
a forgatás a hordozáson keresztül a forgatás művelet egyik változata, ahol a (mindkét végén) eltolt bit a carry zászló régi értéke, a (másik végén) eltolt bit pedig a carry zászló új értékévé válik.
egyetlen forgatás a hordozáson keresztül szimulálhatja egy pozíció logikai vagy aritmetikai eltolódását a hordozási zászló előzetes beállításával. Például, ha a carry jelző 0-t tartalmaz, akkor a x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE logikai jobb eltolás, ha a carry jelző a sign bit másolatát tartalmazza, akkor a x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE egy aritmetikai jobb eltolás. Emiatt néhány mikrokontroller, mint például a low end PICs, csak forgatni és forgatni a hordozáson keresztül, és nem zavarja az aritmetikai vagy logikai eltolási utasításokat.
A rotate through carry különösen akkor hasznos, ha a processzor natív szóméreténél nagyobb számokon hajtunk végre váltásokat, mert ha egy nagy számot két regiszterben tárolunk, akkor az első regiszter egyik végéről eltolt bitnek a második végén kell bejönnie. A rotate-through-carry, hogy kicsit “mentett” a carry zászló alatt az első műszak, készen áll a váltás során a második műszak nélkül extra előkészítés.
magas szintű nyelvekenszerkesztés
C-familyEdit
a C-család nyelveiben a logikai eltolás operátorai “<<” a bal eltolásnál és “>>” a jobb eltolásnál. A váltandó helyek száma a második argumentumként kerül megadásra az operátor számára. Például,
x = y << 2;
x hozzárendeli a y balra történő eltolásának eredményét két bittel, ami egyenértékű a néggyel való szorzással.
az eltolódások implementáció által definiált viselkedést vagy meghatározatlan viselkedést eredményezhetnek, ezért óvatosan kell eljárni a használatuk során. A szó méretével nagyobb vagy egyenlő bitszámmal történő eltolás eredménye meghatározatlan viselkedés a C és C++nyelvben. A negatív érték jobb oldali eltolása implementáció által definiált, és a helyes kódolási gyakorlat nem ajánlja; az aláírt érték bal oldali eltolásának eredménye nincs meghatározva, ha az eredmény nem ábrázolható az eredménytípusban.
a C# – ban a jobb oldali eltolás aritmetikai eltolás, ha az első operandus int vagy hosszú. Ha az első operandus uint vagy ulong típusú, akkor a jobb váltás logikai váltás.
Circular shiftsEdit
a C-nyelvcsaládból hiányzik a rotációs operátor, de a váltási operátorokból szintetizálható. Ügyelni kell arra, hogy a nyilatkozat jól formált legyen, hogy elkerülje a meghatározatlan viselkedést és az időzítési támadásokat a biztonsági követelményekkel rendelkező szoftverekben. Például egy naiv megvalósítás, amely balra forog egy 32 bites előjel nélküli érték x által n pozíciók egyszerűen:
uint32_t x = ..., n = ...;uint32_t y = (x << n) | (x >> (32 - n));
a 0 bittel történő eltolás azonban meghatározatlan viselkedést eredményez a (x >> (32 - n)) jobb oldali kifejezésben, mivel a 32 - 0 32, a 32 pedig a tartományon kívül esik. Egy második próbálkozás eredményezheti:
uint32_t x = ..., n = ...;uint32_t y = n ? (x << n) | (x >> (32 - n)) : x;
ahol a shift összeget tesztelik annak biztosítására, hogy ne vezessen be meghatározatlan viselkedést. Az ág azonban hozzáad egy további kód elérési utat, és lehetőséget kínál az időzítés elemzésére és támadására, ami gyakran nem elfogadható a nagy integritású szoftverekben. Ezenkívül a kód több gépi utasításra fordít, ami gyakran kevésbé hatékony, mint a processzor natív utasítása.
a GCC és a Clang alatti meghatározatlan viselkedés és ágak elkerülése érdekében a következőket javasoljuk. A mintát sok fordító felismeri, és a fordító egyetlen forgatási utasítást bocsát ki:
uint32_t x = ..., n = ...;uint32_t y = (x << n) | (x >> (-n & 31));
vannak olyan fordító-specifikus intrinsics is, amelyek körkörös eltolódásokat hajtanak végre, például _rotl8, _rotl16, _rotr8, _rotr16 a Microsoft Visual C++ – ban. A Clang bizonyos rotate intrinsics-t biztosít a Microsoft kompatibilitásához, amely a fenti problémákat szenvedi el. A GCC nem kínál forgatható belső elemeket. Az Intel x86 belső elemeket is kínál.
JavaEdit
a Java-ban minden egész típus elő van írva, így a “<<” és a “>> ” operátorok aritmetikai eltolásokat hajtanak végre. A Java hozzáadja a “>>>” operátort a logikai jobb eltolások végrehajtásához, de mivel a logikai és aritmetikai bal eltolás műveletek megegyeznek az aláírt egész számokkal, a Java-ban nincs “<<<” operátor.
további részletek A Java shift operátorokról:
- a
<<(bal shift),>>(aláírt jobb shift) és>>>(aláíratlan jobb shift) operátorokat shift operátoroknak nevezzük. - a shift kifejezés típusa a bal oldali operandus előléptetett típusa. Például a
aByte >>> 2egyenértékű((int) aByte) >>> 2. - ha a bal oldali operandus előléptetett típusa int, akkor csak a jobb oldali operandus öt legalacsonyabb rendű bitjét használják eltolási távolságként. Ez olyan, mintha a jobb oldali operandust bitenként logikai és operátor & -nek vetnénk alá 0x1f (0b11111) maszkértékkel. A ténylegesen alkalmazott eltolási távolság tehát mindig a 0-31 tartományban van, beleértve.
- ha a bal oldali operandus előléptetett típusa hosszú, akkor csak a jobb oldali operandus hat legalacsonyabb rendű bitjét használjuk eltolási távolságként. Ez olyan, mintha a jobb oldali operandust bitenként logikai és operátor & -nek vetnénk alá 0x3f (0b111111) maszkértékkel. A ténylegesen alkalmazott eltolási távolság tehát mindig a 0-tól 63-ig terjedő tartományban van.
- a
n >>> sértéke n jobbra eltolt s bitpozíció nulla kiterjesztéssel. - bit és shift műveletekben a
bytetípus implicit módonint– ra konvertálódik. Ha a bájt értéke negatív, akkor a legmagasabb bit egy, akkor az INT-ben lévő extra bájtok kitöltésére szolgálnak. TehátB1 = -5 bájt; int i = b1 / 0x0200;eredményei == -5.
JavaScriptEdit
a JavaScript bitenkénti műveleteket használ a két vagy több egység 1-re vagy 0-ra helyezésének értékelésére.
PascalEdit
a Pascalban és annak minden dialektusában (mint például az Object Pascal és a Standard Pascal) a logikai bal és jobb shift operátorok a “shl” és a “shr“. A shr még aláírt egész számok esetén is logikai eltolódásként viselkedik, és nem másolja a jelbitet. A váltandó helyek száma a második argumentum. Például a következő rendel x az Y balra tolásának eredménye két bittel:
x := y shl 2;