szárazföldi áramlás (vagy felszíni lefolyás) két esetben fordul elő:
1. amikor a felszínre jutó csapadék intenzitása meghaladja a talaj beszivárgási képességét. Ezt a folyamatot Hortoni szárazföldi áramlásnak nevezik.
2. amikor a csapadék intenzitásának és időtartamának kombinációja (és a magasabb területekről történő futás) telíti a talajt, és felemeli a talajvizet a felszínre. Ezt a folyamatot nevezik telítettség szárazföldi áramlás.
esettanulmányok: Hollandia; Belgium; Spanyolország; Kenya; Ghána, Kenya és Mali
Lásd még:
- mosogatók
- Hortoni és telítettség szárazföldi áramlás (beszivárgás)
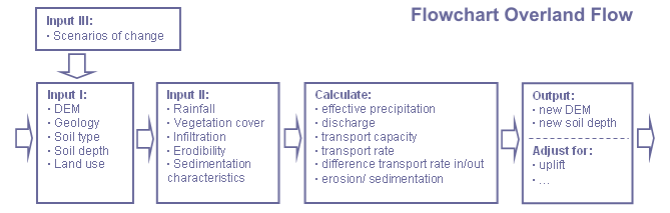
Műszaki információk
a modell vízeróziós és ülepedési moduljának két alapvető feltételezése van: 1) a felszíni vízáramlás potenciális energiája az üledék szállításának hajtóereje és 2) a rácscella üledékbevitele és kimenete közötti különbség megegyezik a tárolás nettó növekedésével (az üledék mozgásának folytonossági egyenlete) (Schoorl et al., 2000). A folyamat leírása Kirkby (Kirkby, 1971) és Foster and Meyer (Foster and Meyer, 1972a; Foster and Meyer, 1972b) korai munkáiból származik, akik 2D képleteket használnak a vízerózió és az ülepedés kiszámításához. A LAPSUS modellhez a képleteket úgy alakították ki, hogy képesek legyenek szimulálni a térbeli (3D) vízeróziót és ülepedést (Schoorl et al., 2000). Az alábbiakban tárgyalt képletek Kirkby, Foster és Meyer 2D képletein alapulnak ,valamint a kísérő egységekkel (Foster és Meyer, 1972a; Foster és Meyer, 1972b; Kirkby, 1971).
a Q ürítés kiszámítása után a rácscellában a C üledékszállítási kapacitás (m2 idő-1) kiszámítható a kibocsátás és a lejtés függvényében:
(1.1) C = 6045>ahol a lejtés gradiense (Z/X) (-) és m (-) és n (-) állandók, amelyek jelzik a vizsgált rendszert: m = 0 és n = 1 a talaj kúszására utal, míg m = n = 3 nagy folyókra utal (Kirkby, 1971). Szigorú határokat nem lehet megadni, mivel az m és n hatása a többi modellparaméterrel való kölcsönhatástól függ. A próbabábu változó (dummy) az egységek korrigálására szolgál.
az S üledékszállítási sebességet (m2 idő-1) az üledék mozgásának integrált folytonossági egyenlete (Eq. 1.2 és 1.3). A képletben használt e-teljesítmény kifejezés összetétele a már S0 szállításban lévő üledék szállítási sebessége (m2 idő-1) (A rácscellában lévő összes magasabb szomszéd bejövő üledékáramai) és a C üledék szállítási kapacitása közötti egyensúlytól függ: ha S0 < C erózió eredménye, míg amikor S0 > C üledékképződés eredménye. A rácscella erodálásakor az S üledékszállítási sebességre a következő képletet kell használni:
(1.2) S = C + (S0 – C) * e-dx * D / C
amikor az üledékek lerakódnak a rácscellában, az S üledékszállítási sebességre a következő képletet használjuk:
(1.3) S = C + ·S0-C)·e-dx * T/C
ahol az S üledék DX (m) rácscellaméret feletti szállítási sebességét úgy számítják ki, hogy összehasonlítják a C üledékszállítási kapacitást a már S0 szállításban lévő üledék szállítási sebességével (m2 idő-1) mínusz a C üledékszállítási kapacitással, amelyet a rácscellák méretéből, a D leválasztási kapacitásból vagy a T ülepedési kapacitásból és a C üledékszállítási kapacitásból eredő e-teljesítménnyel redukálnak.
D leválasztási kapacitás (M idő-1), amely azt mutatja, hogy az üledék mennyire könnyen erodálódik a felületen, a kisülés és a lejtés függvényében számítják ki:
(1.4) D = kes·Q * 6045>
ahol a Kes (m-1) A felület erodálhatóságát jelző halmozott felületi tényező. Települési kapacitás T (M idő-1), amely azt mutatja, hogy az üledék milyen könnyen rakódik le a felszínen, a következőképpen számítják ki:
(1.5) D = Pes * Q * 6045>
ahol a Pes (m-1) egy felületi tényező, amely a halmozott ülepedési jellemzőket jelzi.
ha összehasonlítjuk a rácscella s üledéktranszport-sebességét a már transzportban lévő üledékkel S0 a DS üledéktranszport-sebesség változása, így az erózió vagy az üledékképződés a következőképpen számítható ki:
(1.6) dS = S-S0
a dS újraszámolható erózióra vagy ülepedésre méterben úgy, hogy elosztjuk a rács hosszával dx (m) és megszorozzuk az időlépéssel (idő). A kapott érték a digitális magasságmodell és a talajmélység-térkép korrigálására szolgál a következő időlépéshez.
az e-teljesítmény összehasonlítása határozza meg, hogy a C szállítási kapacitás és az S üledék szállítási sebessége közötti különbség mekkora részét lehet “kielégíteni” a rácscellában. Az érintett változók értékeitől függően az e-teljesítmény eredménye 0 és 1 között változik. Szélsőséges helyzetekben, amikor a dx és a D/T együttesen sokkal nagyobbak, mint C, az e-teljesítmény megközelíti a nullát, és az S üledék szállítási sebessége megegyezik a C üledék szállítási kapacitásával. A másik végletben azonban, amikor a dx és a D/T együttesen sokkal kisebbek, mint a C, az e-teljesítmény megközelíti az 1-et, és az S üledékek szállítási sebessége megegyezik az S0 szállításban már lévő üledékek szállítási sebességével, és nem következik be erózió vagy lerakódás. Kevésbé szélsőséges helyzetekben a modell valószínűleg a C szállítási kapacitáshoz közeli s üledékszállítási sebességet szimulálja. abban az esetben, ha S0 > C több üledéket szállítanak, mint amennyit a fenti rácscellák alapján megengednének, és kevesebb, mint a maximális üledék rakódik le. Az e-teljesítmény ezért alulkoncentrált és szuperkoncentrált áramlásokat eredményez a modellben, simítva az eróziót és a lejtőn történő lerakódást. Nyilvánvaló, hogy az E-power összehasonlítás eredménye nagyon befolyásolja az eróziót és az ülepedést. EQ Összehasonlítása. 1.1 és 1.4/1.5 nyilvánvaló, hogy a kisülés és a lejtés mind a C szállítási kapacitásban, mind a D leválasztási kapacitás vagy a T elszámolási kapacitás számításaiban részt vesz. Mivel a rácscella mérete állandó érték, a kes erodibilitás és a PES ülepedési képesség a legfontosabb változók alacsony m és n értékű helyzetben. Ha m és n nagyobb, akkor a C szállítási kapacitás hatása az E-power kifejezésre növekszik. Az e-power kifejezés eredményét ebben a helyzetben nehezebb megjósolni.