
















Timsort: egy nagyon gyors , O(n log n), stabil rendezési algoritmus, amely a Való Világ számára készült — nem az egyetemen készült.
kattintson ide a frissített cikk megtekintéséhez:

a Timsort egy valós adatokhoz hatékony rendezési algoritmus, amelyet nem tudományos laboratóriumban hoztak létre. Tim Peters 2001-ben hozta létre a Timsort a Python programozási nyelvhez. A Timsort először elemzi a rendezni kívánt listát, majd a lista elemzése alapján választ egy megközelítést.
az algoritmus feltalálása óta alapértelmezett rendezési algoritmusként használják Pythonban, Java-ban, az Android platformon és a GNU Octave-ban.
Timsort nagy O jelölése O (n log n). Ha többet szeretne megtudni a Big O jelölésről, olvassa el ezt.

a Timsort rendezési ideje megegyezik a Mergesortéval, ami gyorsabb, mint a legtöbb más fajta, amelyet ismerhet. A Timsort valójában a beszúrási rendezés és a Mergesort használatát használja, Amint hamarosan látni fogja.
Peters úgy tervezte meg a Timsort, hogy már megrendelt elemeket használjon, amelyek a legtöbb valós adatkészletben léteznek. Ezeket a már megrendelt elemeket “természetes futásoknak”nevezi. Iterálja az elemeket futásokba gyűjtő adatokat, és egyidejűleg egyesíti ezeket a futásokat.
a tömb kevesebb, mint 64 elemet tartalmaz
ha a rendezni kívánt tömb kevesebb, mint 64 elemet tartalmaz, a Timsort beillesztési rendezést hajt végre.
a beszúrási rendezés egy egyszerű rendezés, amely a leghatékonyabb a kis listákon. Nagyobb listáknál elég lassú, de kis listákkal nagyon gyors. A beillesztési rendezés ötlete a következő:
- nézd meg az elemeket egyenként
- a rendezett lista felépítése az elem megfelelő helyre történő beszúrásával
itt található egy nyomkövetési táblázat, amely bemutatja, hogyan rendezné a beillesztési rendezés a listát

ebben az esetben az újonnan rendezett elemeket egy új altömbbe illesztjük be, amely a tömb elején kezdődik.
itt egy gif mutatja beszúrási rendezés:
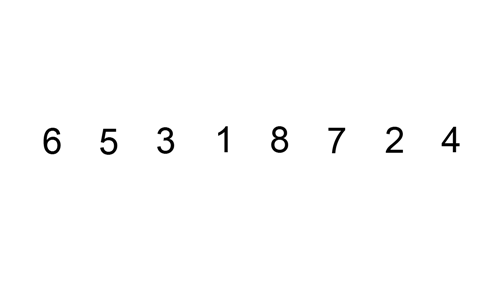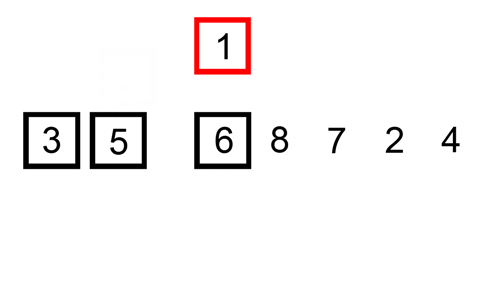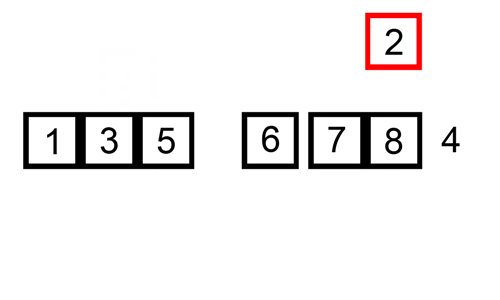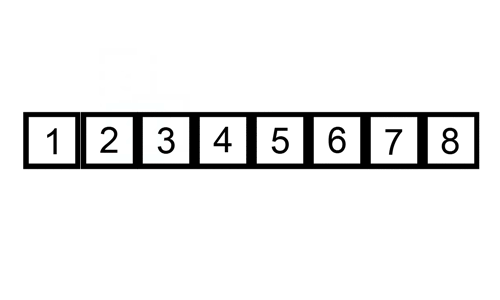
További információ a futtatásokról
ha a lista nagyobb, mint 64 elem, mint az algoritmus először áthalad a listán, szigorúan növekvő vagy csökkenő részeket keresve. Ha a rész csökken, akkor megfordítja azt a részt.
tehát ha a futás csökken, akkor így fog kinézni (ahol a futás félkövér):

ha nem csökken, akkor így fog kinézni:

a minrun egy olyan méret, amelyet a tömb mérete alapján határoznak meg. Az algoritmus úgy választja ki, hogy a legtöbb véletlenszerű tömbben fut, vagy minrun lesz, hosszúságú. Összevonása 2 tömbök hatékonyabb, ha a futások száma egyenlő, vagy valamivel kevesebb, mint, két teljesítmény. Timsort a minrun-t választja, hogy megpróbálja biztosítani ezt a hatékonyságot, ügyelve arra, hogy a minrun egyenlő vagy kisebb legyen, mint kettő.
az algoritmus a minrun-t a 32-től 64-ig terjedő tartományból választja ki. Úgy választja a minrun-t, hogy az eredeti tömb hossza, ha elosztjuk minrun-nal, egyenlő vagy valamivel kisebb, mint kettő.
ha a futás hossza kisebb, mint minrun, akkor kiszámítja a minruntól való futás hosszát. Ezzel az új számmal megragad sok elemet a futtatás előtt, és beillesztési rendezést hajt végre egy új Futtatás létrehozásához.
tehát ha minrun 63, és a futás hossza 33, akkor 63-33 = 30. Ezután megragad 30 elemet a futás vége előtt, tehát ez 30 elem a futásból, majd beillesztési rendezést hajt végre egy új Futtatás létrehozásához.
miután ez a rész befejeződött, most egy csomó rendezett futást kell tartalmaznunk egy listában.
egyesülés

Timsort most végzi mergesort egyesíteni a fut együtt. Azonban a Timsort gondoskodik arról, hogy fenntartsa a stabilitást és az egyesítési egyensúlyt az egyesítési rendezés során.
a stabilitás fenntartása érdekében nem szabad 2 azonos értékű számot cserélnünk. Ez nemcsak megtartja eredeti pozícióikat a listában, hanem lehetővé teszi az algoritmus gyorsabbá tételét. Hamarosan megvitatjuk az egyesítési egyensúlyt.
amint a Timsort fut, hozzáadja őket egy veremhez. Egy egyszerű verem így nézne ki:

Képzeljen el egy halom lemezt. A lemezeket nem lehet alulról venni, ezért felülről kell venni őket. Ugyanez igaz a veremre is.
a Timsort két versengő igényt próbál egyensúlyba hozni, amikor a Mergesort fut. Egyrészt szeretnénk a lehető leghosszabb ideig késleltetni az egyesülést, hogy kihasználhassuk a később felmerülő mintákat. De még inkább szeretnénk a lehető leghamarabb elvégezni az egyesítést, hogy kihasználjuk azt a futást, amelyet az imént talált Futtatás még mindig magas a memória hierarchiájában. Nem késleltethetjük a “túl hosszú” egyesítést sem, mert memóriát igényel, hogy emlékezzen a még nem összekapcsolt futásokra, és a verem rögzített méretű.
a kompromisszum biztosítása érdekében a Timsort nyomon követi a verem három legutóbbi elemét, és két törvényt hoz létre, amelyeknek igaznak kell lenniük ezekre az elemekre:
1. A > B + C
2. B > C
ahol A, B és C a verem három legutóbbi eleme.
maga Tim Peters szavaival:
ami jó kompromisszumnak bizonyult, két invariánst tart fenn a verem bejegyzésein, ahol A, B és C A három jobb oldali, még nem egyesített szelet hossza
általában a különböző hosszúságú szomszédos futások összevonása nehéz. Ami még nehezebbé teszi, hogy meg kell őriznünk a stabilitást. Ennek megkerülése érdekében Timsort félreteszi az ideiglenes memóriát. A kettő közül a kisebbet (mind a futást, mind a B-t hívva) ebbe az ideiglenes memóriába helyezi.
vágtató

míg a Timsort egyesíti a és B, észreveszi, hogy egy futás sokszor egymás után “nyert”. Ha kiderül, hogy az a futás teljesen kisebb számokból áll, mint a B futás, akkor az A futás az eredeti helyére kerül. A két futás összevonása sok munkát jelentene a semmi elérése érdekében.
gyakrabban, mint nem, az adatok valamilyen már létező belső struktúrával rendelkeznek. Timsort feltételezi, hogy ha sok a Futtatás értéke alacsonyabb, mint a Futtatás B értéke, akkor valószínű, hogy A továbbra is kisebb értékekkel rendelkezik, mint B.
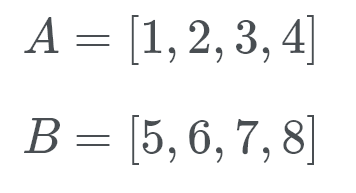
a Timsort ezután vágtató módba lép. Ahelyett, hogy ellenőrizné A és B egymás ellen, a Timsort bináris keresést hajt végre a megfelelő pozícióra b ban ben a. ily módon a Timsort az a egész szakaszát a helyére tudja mozgatni. Ezután a Timsort megkeresi az a megfelelő helyét B-ben.
lássuk ezt működés közben. Timsort ellenőrzi B (ami 5), és egy bináris keresés úgy néz ki, a megfelelő helyen A.
nos, B tartozik a lista végén A. Most Timsort ellenőrzi A (ami 1) a megfelelő helyen B. tehát keresünk, hogy hol a szám 1 megy. Most már tudjuk, hogy B az A végéhez, A pedig a B elejéhez tartozik.
kiderült, hogy ez a művelet nem éri meg, ha a B megfelelő helye nagyon közel van az a elejéhez (vagy fordítva). tehát a galopp mód gyorsan kilép, ha nem fizet ki. Ezenkívül a Timsort tudomásul veszi, és megnehezíti a galopp módba való későbbi belépést azáltal, hogy növeli a belépéshez szükséges egymást követő A-vagy csak B-győzelmek számát. Ha a galopp mód megtérül, a Timsort megkönnyíti az újbóli belépést.
röviden, Timsort nem 2 dolog hihetetlenül jól:
- nagyszerű teljesítmény a már létező belső struktúrájú tömbökön
- stabil rendezést lehet fenntartani
korábban a stabil rendezéshez a listában szereplő elemeket egész számokkal kell feltölteni, és sorszámként rendezni.
Kód
ha nem érdekli a kód, nyugodtan hagyja ki ezt a részt. Van még néhány információ a szakasz alatt.
az alábbi forráskód az enyém és Nanda Javarma munkáján alapul. A forráskód nem teljes, és nem is hasonlít a Python hivatalos rendezett () forráskódjához. Ez csak egy lebutított Timsort valósítottam meg, hogy általános hangulatot szerezzek a Timsort-ról. Ha a Timsort eredeti forráskódját teljes dicsőségében szeretné látni, nézze meg itt. A Timsort hivatalosan C-ben hajtják végre, nem Pythonban.
a Timsort valójában közvetlenül a Pythonba van beépítve, tehát ez a kód csak magyarázóként szolgál. A Timsort használatához egyszerűen írjon:
list.sort()
vagy
sorted(list)
ha szeretné elsajátítani a Timsort működését, és meg akarja érezni, nagyon javaslom, hogy próbálja meg saját maga megvalósítani!
ez a cikk Tim Peters eredeti bevezetésén alapul Timsort, itt található.