Logaritmi: Introduzione a “La Relazione”

Ritorno all’Indice Lezioni | Fare le Lezioni in Ordine di Stampa | -friendly pagina

Logaritmi: Introduzione
“Rapporto” (pagina 1 di 3)

Sezioni: Introduzione ai registri, Semplificando il registro di espressioni Comuni e naturali registri

Logaritmi sono “contrario” di esponenziali, proprio come la sottrazione è l’opposto di addizione e la divisione è l’opposto di moltiplicazione. Registri esponenziali” annulla”. Tecnicamente parlando, i log sono gli inversi degli esponenziali.

In termini pratici, l’ho trovato utile pensare registri in termini di Rapporto:

Sul lato sinistro sopra c’è l’istruzione esponenziale “y = bx”. Sul lato destro sopra, “logb (y) = x” è l’istruzione logaritmica equivalente, che si pronuncia “log-base-b di y uguale a x”; Il valore del subscripted “b” è “la base del logaritmo”, proprio come b è la base nell’espressione esponenziale “bx”. E, proprio come la base b in un esponenziale è sempre positiva e non uguale a 1, così anche la base b per un logaritmo è sempre positiva e non uguale a 1. Qualunque cosa sia all’interno del logaritmo è chiamato “argomento” del log. Si noti che la base sia nell’equazione esponenziale che nell’equazione di log (sopra) è “b”, ma che x e y cambiano i lati quando si passa tra le due equazioni.

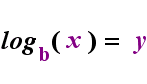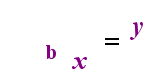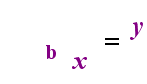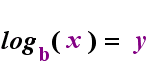
Se si può ricordare questa relazione (che, qualunque fosse stato l’argomento del log diventa il “uguale a” e qualsiasi cosa fosse stata “è uguale a” diventa l’esponente esponenziale, e viceversa), quindi non dovrebbe avere troppi problemi con l’uso dei logaritmi.

(Ho coniato io stesso il termine “La relazione”. Non lo troverai nel tuo testo, e i tuoi insegnanti e tutor non avranno idea di cosa stai parlando se lo menzioni a loro. “La relazione” è una terminologia del tutto non standard. Perché lo uso comunque? Perché funziona.)

A proposito: se hai notato che ho cambiato le variabili tra le due caselle che mostrano “La relazione”, hai un occhio acuto. L’ho fatto apposta, per sottolineare che il punto non sono le variabili stesse, ma come si muovono.

• Converti “63 = 216” nell’espressione logaritmica equivalente.

Per convertire, la base (cioè il 6)rimane la stessa, ma il 3 e il 216 cambiano i lati. Questo mi dà:

log6(216) = 3 Copyright © Elizabeth Stapel 2002-2011 Tutti i diritti riservati

• Converti “log4(1024) = 5” nell’espressione esponenziale equivalente.

Per convertire, la base (cioè il 4) rimane la stessa, ma il 1024 e il 5 cambiano i lati. Questo mi dà:

45 = 1024

In alto| 1 | 2 | 3 | Torna all’indice successivo >>