
















Timsort: Un algoritmo di ordinamento stabile molto veloce , O(n log n), costruito per il mondo reale — non costruito nel mondo accademico.
Clicca qui per vedere l’articolo aggiornato:

Timsort è un algoritmo di ordinamento che è efficiente per i dati del mondo reale e non creato in un laboratorio accademico. Tim Peters ha creato Timsort per il linguaggio di programmazione Python nel 2001. Timsort prima analizza l’elenco che sta cercando di ordinare e quindi sceglie un approccio basato sull’analisi dell’elenco.
Poiché l’algoritmo è stato inventato, è stato utilizzato come algoritmo di ordinamento predefinito in Python, Java, la piattaforma Android e in GNU Octave.
La notazione Big O di Timsort è O(n log n). Per conoscere la notazione Big O, leggi questo.

Il tempo di ordinamento di Timsort è lo stesso di Mergesort, che è più veloce della maggior parte degli altri tipi che potresti conoscere. Timsort fa effettivamente uso di Insertion sort e Mergesort, come vedrai presto.
Peters ha progettato Timsort per utilizzare elementi già ordinati che esistono nella maggior parte dei set di dati del mondo reale. Chiama questi elementi già ordinati “corse naturali”. Itera i dati raccogliendo gli elementi in esecuzioni e contemporaneamente unendo quelle esecuzioni insieme in uno.
L’array contiene meno di 64 elementi
Se l’array che stiamo cercando di ordinare contiene meno di 64 elementi, Timsort eseguirà un ordinamento di inserimento.
Un ordinamento di inserimento è un ordinamento semplice che è più efficace su piccole liste. È piuttosto lento nelle liste più grandi, ma molto veloce con piccole liste. L’idea di un ordinamento per inserzione è come indicato di seguito:
- Guarda elementi uno per uno
- Costruire la lista ordinata inserendo l’elemento nella posizione corretta
Qui c’è una tabella di traccia che mostra come ordinamento per inserzione vorrei ordinare l’elenco

In questo caso stiamo inserendo gli elementi appena ordinati in un nuovo sub-array, che inizia all’inizio dell’array.
Ecco una gif che mostra l’ordinamento di inserimento:
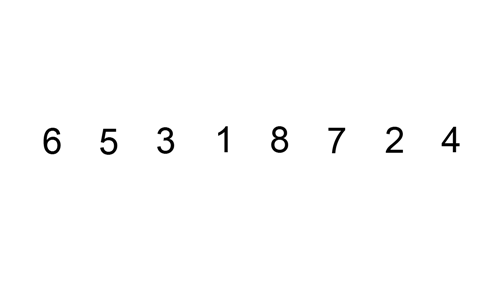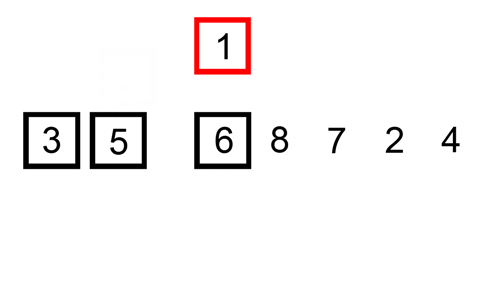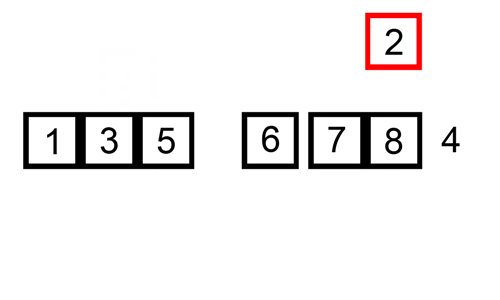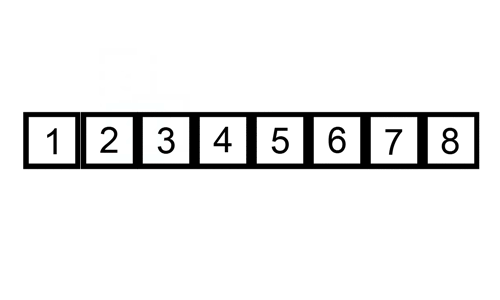
Maggiori informazioni sulle esecuzioni
Se l’elenco è più grande di 64 elementi rispetto all’algoritmo farà un primo passaggio attraverso l’elenco alla ricerca di parti che sono rigorosamente in aumento o in diminuzione. Se la parte sta diminuendo, invertirà quella parte.
Quindi se la corsa sta diminuendo, sarà simile a questa (dove la corsa è in grassetto):

Se non diminuisce, sarà simile a questo:

Il minrun è una dimensione che viene determinata in base alla dimensione dell’array. L’algoritmo lo seleziona in modo che la maggior parte delle esecuzioni in un array casuale siano o diventino minrun in lunghezza. L’unione di 2 array è più efficiente quando il numero di esecuzioni è uguale o leggermente inferiore a una potenza di due. Timsort sceglie minrun per cercare di garantire questa efficienza, assicurandosi che minrun sia uguale o inferiore a una potenza di due.
L’algoritmo sceglie minrun dall’intervallo da 32 a 64 incluso. Sceglie minrun in modo tale che la lunghezza dell’array originale, se divisa per minrun, sia uguale o leggermente inferiore a una potenza di due.
Se la lunghezza della corsa è inferiore a minrun, si calcola la lunghezza di quella fuga da minrun. Utilizzando questo nuovo numero, si afferrano molti elementi prima della corsa ed eseguire un ordinamento di inserimento per creare una nuova corsa.
Quindi se minrun è 63 e la lunghezza della corsa è 33, fai 63-33 = 30. Quindi prendi 30 elementi da davanti alla fine della corsa, quindi si tratta di 30 elementi da esegui e quindi esegui un ordinamento di inserimento per creare una nuova esecuzione.
Dopo che questa parte è stata completata, ora dovremmo avere un gruppo di esecuzioni ordinate in un elenco.
Fusione

Timsort ora esegue mergesort per unire le esecuzioni insieme. Tuttavia, Timsort si assicura di mantenere la stabilità e l’equilibrio dell’unione durante l’ordinamento dell’unione.
Per mantenere la stabilità non dovremmo scambiare 2 numeri di uguale valore. Questo non solo mantiene le loro posizioni originali nell’elenco, ma consente all’algoritmo di essere più veloce. Discuteremo a breve il bilancio delle fusioni.
Quando Timsort trova le esecuzioni, le aggiunge a uno stack. Una semplice pila sarebbe simile a questa:

Immagina una pila di piastre. Non puoi prendere i piatti dal basso, quindi devi prenderli dall’alto. Lo stesso vale per una pila.
Timsort tenta di bilanciare due esigenze concorrenti quando viene eseguito mergesort. Da un lato, vorremmo ritardare la fusione il più a lungo possibile per sfruttare i modelli che potrebbero sorgere in seguito. Ma vorremmo ancora di più fare la fusione il prima possibile per sfruttare la corsa che la corsa appena trovata è ancora alta nella gerarchia della memoria. Inoltre, non possiamo ritardare la fusione “troppo a lungo” perché consuma memoria per ricordare le esecuzioni che sono ancora non riunite e lo stack ha una dimensione fissa.
Per essere sicuri di avere questo compromesso, Timsort tiene traccia dei tre elementi più recenti in pila e crea due leggi che devono valere per tali elementi:
1. A > B + C
2. B > C
Dove A, B e C sono i tre elementi più recenti nello stack.
Nelle parole dello stesso Tim Peters:
Quello che si è rivelato essere un buon compromesso mantiene due invarianti sulle voci dello stack, dove A, B e C sono le lunghezze delle tre sezioni più a destra non ancora unite
Di solito, unire le esecuzioni adiacenti di lunghezze diverse sul posto è difficile. Ciò che rende ancora più difficile è che dobbiamo mantenere la stabilità. Per aggirare questo problema, Timsort mette da parte la memoria temporanea. Posiziona il più piccolo (chiamando entrambe le esecuzioni A e B) delle due esecuzioni in quella memoria temporanea.
Galoppo

Mentre Timsort sta unendo A e B, nota che una corsa ha “vinto” molte volte di seguito. Se risultasse che la corsa A consisteva in numeri completamente più piccoli della corsa B, la corsa A sarebbe tornata al suo posto originale. Unire le due esecuzioni comporterebbe molto lavoro per non ottenere nulla.
Il più delle volte, i dati avranno una struttura interna preesistente. Timsort presuppone che se molti valori di run A sono inferiori ai valori di run B, è probabile che A continui ad avere valori più piccoli di B.
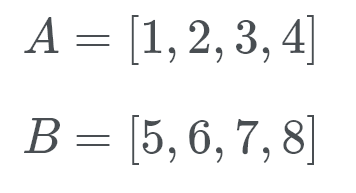
Timsort entrerà quindi in modalità galoppo. Invece di controllare A e B l’uno contro l’altro, Timsort esegue una ricerca binaria per la posizione appropriata di b in a. In questo modo, Timsort può spostare un’intera sezione di A in posizione. Poi Timsort cerca la posizione appropriata di A in B. Timsort sarà quindi spostare un’intera sezione di B può in una sola volta, e in posizione.
Vediamo questo in azione. Timsort controlla B (che è 5) e usando una ricerca binaria cerca la posizione corretta in A.
Beh, B appartiene alla parte posteriore della lista di A. Ora Timsort controlla A (che è 1) nella posizione corretta di B. Quindi stiamo cercando di vedere dove va il numero 1. Questo numero va all’inizio di B. Ora sappiamo che B appartiene alla fine di A e A appartiene all’inizio di B.
Si scopre che questa operazione non vale la pena se la posizione appropriata per B è molto vicina all’inizio di A (o viceversa). quindi la modalità galoppo esce rapidamente se non sta dando i suoi frutti. Inoltre, Timsort prende nota e rende più difficile entrare in modalità galoppo in seguito aumentando il numero di vittorie consecutive solo A o solo B necessarie per entrare. Se la modalità galoppo sta dando i suoi frutti, Timsort rende più facile rientrare.
In breve, Timsort fa 2 cose incredibilmente bene:
- Grandi prestazioni su array con struttura interna preesistente
- Essere in grado di mantenere un ordinamento stabile
In precedenza, per ottenere un ordinamento stabile, dovresti comprimere gli elementi nella tua lista con numeri interi e ordinarli come un array di tuple.
Codice
Se non sei interessato al codice, sentiti libero di saltare questa parte. C’è qualche informazione in più sotto questa sezione.
Il codice sorgente riportato di seguito è basato sul mio lavoro e sul lavoro di Nanda Javarma. Il codice sorgente non è completo, né è simile al codice sorgente ufficiale ordinato () di Python. Questo è solo un Timsort dumbed-down che ho implementato per avere un’idea generale di Timsort. Se vuoi vedere il codice sorgente originale di Timsort in tutta la sua gloria, dai un’occhiata qui. Timsort è ufficialmente implementato in C, non in Python.
Timsort è effettivamente integrato in Python, quindi questo codice serve solo come spiegatore. Per usare Timsort basta scrivere:
list.sort()
Oppure
sorted(list)
Se vuoi padroneggiare come funziona Timsort e farti un’idea, ti consiglio vivamente di provare a implementarlo da solo!
Questo articolo è basato sull’introduzione originale di Tim Peters a Timsort, trovata qui.