私たちの目的は、重力場のポアソンの方程式の相対論的一般化を見つけることで:
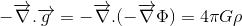
ここで、Φは重力ポテンシャルを指し、θは質量密度を指し、私たちは半分の方法です。
確かに、以前の記事では、質量密度の一般化(方程式の右項)がエネルギー運動量T Μ Vに対応するエネルギー運動量テンソルをすでに見てきました。
私たちの方程式は次の形をとるべきだと仮定するのは合理的です:
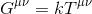
ここで、kはスカラーを表し、G Μ Vはアインシュタインテンソルと呼ばれ、時空の曲率を記述する階数2のテンソルを表す。
私たちが知る限り、G Μ Vは次の制約に従う必要があります:
-フラットな時空で無効にする必要があります
-時空の曲率を記述し、リーマンテンソルに対して線形である必要があります
-対称でランク2(T Μ Vとして)
-ヌル発散を持つ必要があります(T Μ Vとして)
-最後に、ニュートン極限で4ngp
リッチテンソルを解として最初の試み
重力ポテンシャルφはh00=(g00-1)/c2
を介してメトリックの00成分にリンクされていることをニュートン極限における測地方程式から思い出してください。
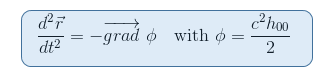
リーマンテンソルの場合である計量の二次導関数を含むテンソルを探すのは自然なようです。 さらに、リーマンテンソルは、時空の曲率を記述することができることをこれまでに知っている唯一の候補です(上記の第2の制約参照)。
ランク2のテンソルを見つけなければならないので、リーマンテンソルだけで解を見つけなければならないと仮定すると、まずリッチテンソルと呼ばれるリーマンテンソルの縮約形を考えるのが自然なようである。
これを見るために、thaの記事The Riemann curvature tensor part II:derivation from the geodesic deviationからリーマンテンソルの式を思い出してみましょう
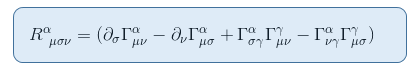
静的および弱い重力場の限界では、1つの項だけがR00に寄与します:
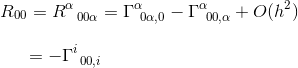
同じ記事では、このChristoffelシンボルを計算し、次のことを発見しました
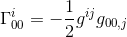
gij=nijとgoo、j=hoo、j(記事を参照)の近似では、次のようになります:
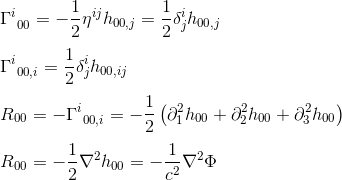
Δ Φ(ラプラシアン作用素)を用いたR00の同定は、一般相対性理論における場の方程式がRabをTabの定数倍と同一視するべきであることを示唆している。
1915年、この方程式を用いて、アインシュタインは水星近日点歳差運動の長年の問題を解決することさえでき、その年の11月に”数日間、私は自分のそばに”
結局、アインシュタインはRabの一般的な発散が無効にならないという事実のために、この最初の試みを拒否しなければならなかった。
第二の試み
リッチスカラーと密接に関連するテンソルがありますwihchは矛盾することなく左側に置くことができます。 これは次のように定義されたアインシュタインテンソルを与える:
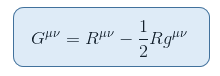
ここで、R=Raaはリッチスカラーまたはスカラー曲率です。
この形式のGabは対称でランク2であり、明らかに時空の曲率を記述します。 したがって、総導関数がゼロであることを示すだけです
これを行うには、Bianchi恒等式から始めます
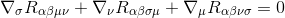
g λ g α λ g β λ(メトリック導関数はゼロであるため、定数として機能し、導関数の内部で取ることができます)を乗算すると、次のようになります:
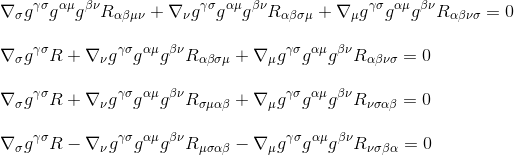
Ricciテンソル定義R Μ V=g β g β r β γを使用して(ステップ3)、インデックスの名前を変更することによって(ステップ4)、次のようになります
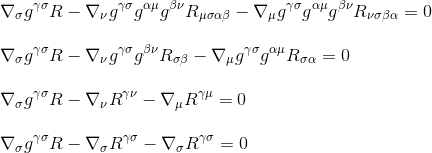
微分を因数分解することによって、我々は最終的に得る
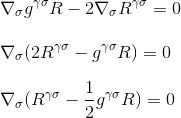
これはまさに私たちが実証したかったことです:アインシュタインテンソルの発散はnullであり、曲率/質量-エネルギー方程式の左側の正しい候補を見つけ