面積慣性モーメントまたは面積の慣性モーメント-面積の第二モーメントとも呼ばれます-Iは、梁のたわみ、曲げ、応力を予測するために使用される形状のプロパティです。メートル単位
- mm4
- cm4
- m4
面積慣性モーメント-メートル単位
- mm4
- m4
面積慣性モーメント-メートル単位
- mm4
- m4
単位間変換
- 1 cm4=10-8m4=104mm4
- 1in4=4.16x105mm4=41.6cm4
例-面積慣性モーメント単位
9240cm4をmm4に変換するには、104
(9240cm4)104=9を掛けることができます。24 107mm4
面積慣性モーメント(面積の慣性モーメントまたは面積の第二モーメント)
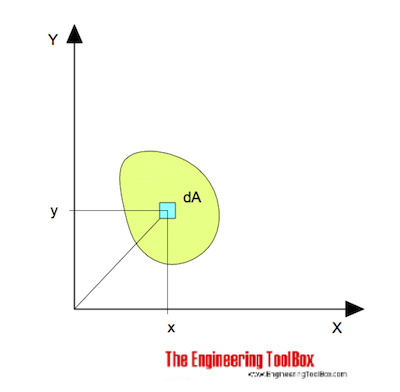
x軸周りの曲げのための
Ix=≤y2dA(1)
ここで、
Ix=x軸に関連する面積慣性モーメント(m4,mm4,inches4)
y=垂直距離軸xから要素da(m、Mm、インチ)まで)
dA=元素面積(m2,mm2,inches2))
曲がることのための慣性モーメント y軸の周りは
iy=≤x2dA(2)
ここで、
Iy=Y軸に関連する面積慣性モーメント(m4,mm4,inches4)
x=軸yから要素dA(m,mm,inches)までの垂直距離
典型的な断面積i
- 典型的な断面の面積慣性モーメントii
固体正方形断面
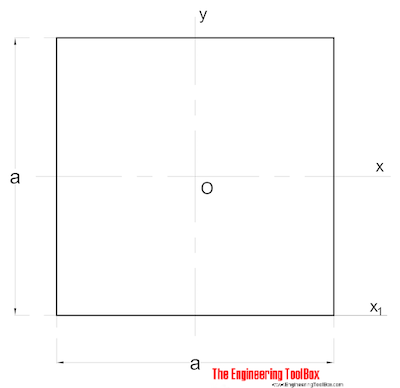
固体正方形断面の面積慣性モーメントは、
ix =a4/ 12 (2)
ここで、
a=side(mm,m,in..)
Iy=a4/12(2b)
固体矩形断面
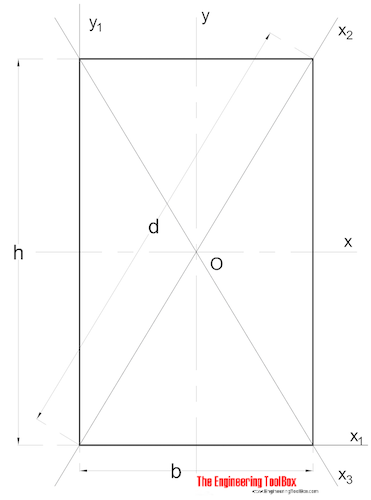
矩形断面のIneriaの面積モーメントは、
Ix=b h3として計算することができます/ 12 (3)
ここで、
b=幅
h=高さ
Iy=b3h/12(3b)
固体円形断面
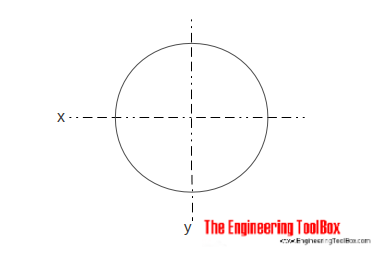
固体円筒断面の面積慣性モーメントは、
Ix=π r4/4
=≤d4/ 64 (4)
ここで、
r=半径
d=直径
Iy=≤r4/4
=≤d4/64(4b)
中空円筒断面
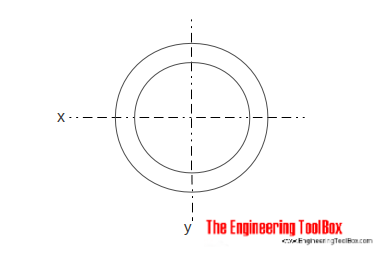
中空円筒断面の面積慣性モーメントは、
Ix=≤(do4-di4) / 64 (5)
ここで、
do=シリンダー外径
di=シリンダー内径
Iy=√(do4-di4)/64(5b)
平方セクション ・対角モーメント
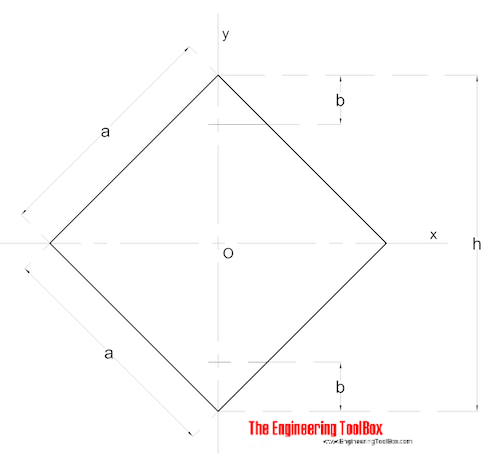
正方形断面の対角面積慣性モーメントは、
Ix=Iy=a4として計算できます/ 12 (6)
長方形断面-重心を通る任意の直線上の面積モーメント
長方形断面および重心を通る直線上のモーメントの面積は、
Ix=(b h/12)(h2cos2a+b2sin2a) (7)
対称形状
面積慣性モーメント-対称形状
面積慣性モーメント-対称形状
面積慣性モーメント-対称形状
面積慣性モーメント 対称形状のセクションは、
Ix=(a h3/12)+(b/12)(H3-h3)として計算できます) (8)
Iy=(a3h/12)+(b3/12)(H-h)(8b)
非対称形状
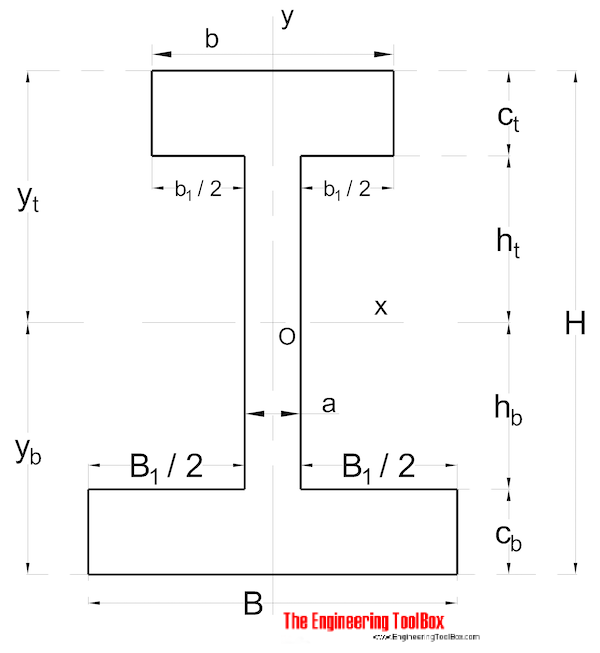
非対称形状セクションの面積慣性モーメントは、
Ix=(1/3)(B)として計算できますYb3-b1hb3+B YT3-b1HT3) (9)
- 代表断面における面積慣性モーメントII
面積慣性モーメント対極慣性モーメント対 慣性モーメント
- “面積慣性モーメント”は、ビームのたわみ、曲げ、応力を予測するために使用される形状の特性であり、
- “極慣性モーメント”は、トルクを受けるビームのねじれを計算するために必要なねじりに抵抗するビームの能力の尺度として、
- “慣性モーメント”は、物体の回転方向の変化に対する抵抗の尺度である。
断面係数
- “断面係数”はW=I/yとして定義され、Iは慣性面積モーメント、yは中性軸から任意の繊維までの距離です。