우리의 목표는 중력장에 대한 푸아송 방정식의 상대 론적 일반화를 찾는 것입니다 경우:
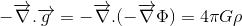
여기서 제 2 차 세계 대전은 중력 잠재력과 제 2 차 세계 대전의 질량 밀도에 대한 제 2 차 세계 대전의 질량 밀도에 대한 제 2 차 세계 대전의 질량 밀도를 나타냅니다.
실제로,우리는 이전 기사에서 질량 밀도의 일반화(방정식의 오른쪽 항)가 에너지-운동량 티 에 해당한다는 에너지-운동량 텐서를 이미 보았습니다.
우리의 방정식의 형태를 취해야한다고 가정하는 것이 합리적인 것 같습니다:
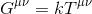
여기서 케이 의미 스칼라 과 지 지 아인슈타인 텐서라는 이름은 시공간 곡률을 설명하는 순위 2 텐서를 나타냅니다.
우리가 아는 한,제 12 조는 다음과 같은 제약을 준수해야합니다.:
-그것은 평면 시공간에서 무효화한다
-그것은 시공간 곡률을 설명하고 리만 텐서에 대해 선형이어야한다
-그것은 대칭이어야하고 랭크 2(으로 티 티 10)
-그것은 널 발산을 가져야한다(으로 티 10)
-그리고 마지막으로,뉴턴의 곡률에 대한 리만 텐서
우리는 뉴턴 한계의 측지 방정식에서 중력 잠재력이 00-구성 요소에 연결되어 있음을 상기합니다.
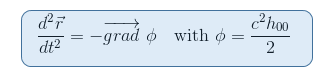
그것은 다음 텐서 리만 텐서의 경우는 메트릭의 두 번째 파생 상품을 포함 하는 보고 자연 보인다. 또한,리만 텐서는 우리가 지금까지 시공간 곡률을 설명 할 수있는 유일한 후보입니다(위의 두 번째 제약 조건 참조).
우리는 순위-2 텐서를 찾을 수 있고,우리는 우리가 전적으로 리만 텐서의 관점에서 솔루션을 찾을 수 있다고 가정하면,먼저 리만 텐서의 계약 형태를 고려하는 것이 자연 보인다,리치 텐서로 알려진.
이를 보려면 리만 텐서의 표현을 상기합시다 그쪽으로 기사 리만 곡률 텐서 2 부:측지 편차로부터의 유도
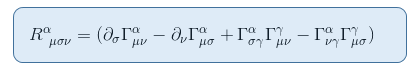
정적 및 약한 중력장의 한계에서 하나의 용어 만 기여 아르 자형 00:
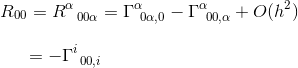
같은 글에서,우리는 이 크리스토펠의 상징을 계산했고,
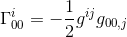
의 근사치로 지=니지 과 끈적 거리는,제이=후,제이(기사 참조)우리는:
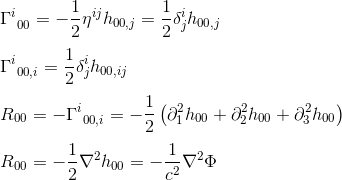
식별 아르 자형 00 와 2000(라플라시안 연산자)는 일반 상대성 이론의 필드 방정식이 라브를 탭의 일정한 배수와 동일시해야한다고 제안합니다.
1915 년,이 방정식을 사용하여,아인슈타인은 심지어 수성 근일점 세차 운동의 오랜 문제를 해결할 수 있었다,그 해 11 월에 작성하는 원인,”며칠 동안,나는 즐거운 흥분과 함께 자신 옆에 있었다.”
결국,아인슈타인은 인해 랩의 일반적인 발산이 무효화되지 않는다는 사실에,이 첫 번째 시도를 거부했다.
두 번째 시도
텐서가 밀접하게 리치 스칼라 위치 모순없이 왼쪽에 넣을 수 있습니다 관련이있다. 이것은 다음과 같이 정의 된 아인슈타인 텐서를 제공합니다:
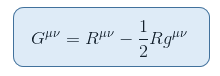
여기서 아르 자형=라아 이다 리치 스칼라 또는 스칼라 곡률.
이러한 형태의 갑은 대칭적이고 랭크-2 이며 시공간 곡률을 분명히 설명합니다. 그래서 그냥 남아있는 파생상품 영
이를 위해,우리가 시작과 함께 가장 핵심적인 부분이라고 할 id
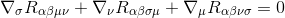
을 곱하여 통해 gγσgαμgβν(메트릭 파생물 제로,그래서 그들은 행동으로 상수 및 취할 수 있습 내부에 파생상품),그 수익률:
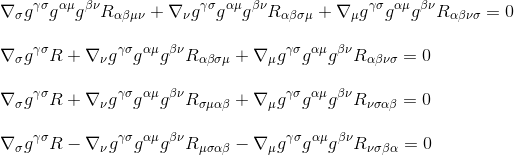
(3 단계)및 인덱스(4 단계)의 이름을 바꿈으로써,우리는 얻을
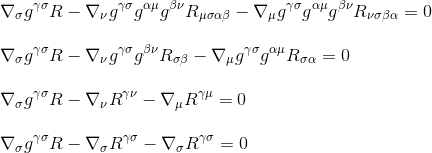
미분을 인수 분해함으로써 우리는 마침내 다음을 얻습니다
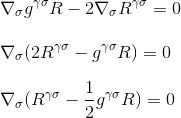
아인슈타인 텐서의 발산은 무효,그리고 우리는 우리의 곡률/질량-에너지 방정식의 왼쪽에 대한 올바른 후보를 발견했습니다.