계산하려면 쉼표로 구분 된 숫자를 제공하십시오.
관련 통계 계산기/표준 편차 계산기/표본 크기 계산기
평균
영어에서 여러 다른 단어에 대한 동음 이의어 인 단어 평균은 수학 영역에서도 유사하게 모호합니다. 문맥에 따라,수학적 또는 통계적 여부,”평균”이 의미하는 것은 바뀝니다. 데이터 세트에 관한 가장 간단한 수학적 정의에서 사용 된 평균은 수학적 기대 또는 평균이라고도하는 산술 평균입니다. 이 형식에서 평균은 개별 숫자 집합 사이의 중간 값,즉 데이터 세트의 모든 값의 합계를 총 값 수로 나눈 값을 나타냅니다. 산술 평균을 계산하는 방정식은 사용 된 변수에 약간의 변화와 함께 모집단 및 표본 평균의 통계적 개념을 계산하는 것과 거의 동일합니다:
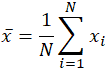
평균은 종종 다음과 같이 표시됩니다 엑스,발음”엑스 바,”그리고 다른 용도에서도 변수가 아닌 경우 엑스,막대 표기법 어떤 형태의 평균의 일반적인 지표입니다. 인구 평균의 특정 경우에,변수를 사용하는 대신 엑스,그리스어 기호 뮤,또는 제 2,사용됩니다. 마찬가지로,또는 다소 혼란스럽게,통계의 표본 평균은 종종 자본으로 표시됩니다. 주어진 데이터 세트 10, 2, 38, 23, 38, 23, 21, 수익률 위의 합계를 적용:
|
10 + 2 + 38 + 23 + 38 + 23 + 21 |
= | = 22.143 |
앞서 언급했듯이 이것은 평균의 가장 간단한 정의 중 하나이며 일부 다른 정의에는 가중치 산술 평균(데이터 세트의 특정 값이 다른 값보다 더 많은 값을 기여한다는 점에서만 다름)과 기하 평균이 포함됩니다. 주어진 상황과 상황에 대한 적절한 이해는 종종 사람에게 통계적으로 관련된 방법을 결정하는 데 필요한 도구를 제공 할 수 있습니다. 일반적으로,평균,중앙값,모드 및 범위는 주어진 샘플 또는 데이터 세트에 대해 이상적으로 모두 계산되고 분석되어야 하며,이는 주어진 데이터의 다른 측면을 명료하게 하기 때문이며,단독으로 고려될 경우,다음 섹션에서 설명될 것처럼 데이터의 허위 진술로 이어질 수 있다.
중앙값
중앙값의 통계적 개념은 데이터 샘플,모집단 또는 확률 분포를 두 부분으로 나누는 값입니다. 중앙값을 찾는 것은 기본적으로 나머지 숫자 사이에 물리적 위치가 있는 데이터 샘플에서 값을 찾는 것과 관련이 있습니다. 유한 숫자 목록의 중앙값을 계산할 때 데이터 샘플의 순서가 중요합니다. 일반적으로 값이 오름차순으로 나열되지만 값을 내림차순으로 나열하는 것이 다른 결과를 제공하는 실제 이유는 없습니다. 데이터 샘플의 총 값 수가 홀수인 경우 중앙값은 단순히 모든 값 목록의 중간에 있는 숫자입니다. 데이터 샘플에 짝수 개의 값이 포함된 경우 중앙값은 두 개의 중간 값의 평균입니다. 이것은 혼란 스러울 수 있지만,중앙값은 때때로 평균의 계산을 포함하지만,이 경우가 발생하면 두 개의 중간 값만 포함되고 평균은 데이터 샘플의 모든 값을 포함한다는 것을 기억하십시오. 두 개의 데이터 샘플만 있거나 모든 값이 동일한 짝수 샘플이 있는 홀수의 경우 평균과 중앙값은 동일합니다. 이전과 동일한 데이터 집합이 주어지면 중앙값은 다음과 같은 방식으로 획득됩니다:
2,10,21,23,23,38,38
데이터를 오름차순으로 나열하고 홀수의 값이 있음을 결정한 후 23 이이 경우에 주어진 중앙값이라는 것이 분명합니다. 데이터 집합에 다른 값이 추가된 경우:
2,10,21,23,23,38,38,1027892
짝수 개의 값이 있기 때문에 중앙값은 두 개의 중간 숫자(이 경우 23 과 23)의 평균이며 평균은 23 입니다. 이 특정 데이터 세트에서 특이치(예상 값 범위를 벗어나는 값)인 값 1,027,892 를 추가하면 데이터 세트에 실제 영향을 미치지 않습니다. 그러나 이 데이터 세트에 대해 평균이 계산되면 결과는 128,505.875 입니다. 이 값은 분명히 평균 및 이상치보다 훨씬 작고 값이 더 가까운 데이터 집합의 다른 7 개 값을 잘 나타내지 않습니다. 이는 평균과 비교할 때 통계 데이터를 설명 할 때 중앙값을 사용하는 주요 이점입니다. 데이터를 설명 할 때 다른 통계 값뿐만 아니라 둘 다 계산해야하지만,하나만 사용할 수있는 경우 값 사이에 매우 큰 변화가있을 때 중앙값은 주어진 데이터 집합에서 일반적인 값의 더 나은 추정치를 제공 할 수 있습니다.
모드
통계에서 모드는 재발 횟수가 가장 많은 데이터 집합의 값입니다. 데이터 집합이 다중 모드일 수 있으므로 둘 이상의 모드가 있습니다. 예를 들어:
2,10,21,23,23,38,38
23 과 38 모두 각각 두 번 나타나 위의 데이터 세트 모드입니다.
평균과 중앙값과 유사하게,이 모드는 확률 변수 및 모집단에 대한 정보를 표현하는 방법으로 사용됩니다. 그러나 평균 및 중앙값과는 달리,이 모드는 식료품 점에서 가장 일반적으로 구입 한 토틸라 칩 브랜드와 같은 비 수치 값에 적용 할 수있는 개념입니다. 예를 들어,토스티토스,미션 및 소치틀의 브랜드를 비교할 때,토스티토스 및 미션 브랜드 토틸라 칩에 비해 토스티토스 및 미션 브랜드 토틸라 칩에 비해 3:2:1 비율로 각각 판매되는 것이 발견되면,이 비율을 사용하여 각 브랜드의 재고 가방 수를 결정할 수 있습니다. 특정 기간 동안 토틸라 칩 24 봉지가 판매되는 경우 상점에서는 소치 틀 칩 12 봉지,토스 티토 스 8 봉지,미션 4 봉지를 사용할 수 있습니다. 그러나 매장은 단순히 평균을 사용하고 판매 한 경우 8 각각의 가방,그것은 잠재적으로 잃을 수 4 고객은 소치 틀 칩이 아닌 다른 브랜드를 원하는 경우 판매. 이 예에서 알 수 있듯이 데이터 샘플에 대한 결론을 도출 할 때 통계 값의 모든 방식을 고려하는 것이 중요합니다.
범위
통계의 데이터 집합 범위는 가장 큰 값과 가장 작은 값의 차이입니다. 범위는 통계와 수학의 다른 영역 내에서 다른 의미를 가지고 있지만,이것은 가장 기본적인 정의이며,제공된 계산기에 의해 사용되는 것입니다. 동일한 예제 사용:
2,10,21,23,23,38,38
38 – 2 = 36
이 예제의 범위는 36 입니다. 평균과 마찬가지로 범위는 매우 크거나 작은 값에 의해 크게 영향을받을 수 있습니다. 이전과 동일한 예제 사용: