vennligst oppgi tall atskilt med komma for å beregne.
Relatert Statistikk Kalkulator | Standardavvik Kalkulator / Sample Size Calculator
Mean
ordet betyr, som er et homonym for flere andre ord på engelsk, er tilsvarende tvetydig selv i matematikkområdet. Avhengig av konteksten, enten matematisk eller statistisk, hva menes med «middel» endringer. I sin enkleste matematiske definisjon om datasett er gjennomsnittet brukt det aritmetiske gjennomsnittet, også referert til som matematisk forventning, eller gjennomsnitt. I dette skjemaet refererer gjennomsnittet til en mellomverdi mellom et diskret sett med tall, nemlig summen av alle verdier i datasettet, dividert med totalt antall verdier. Ligningen for beregning av et aritmetisk gjennomsnitt er nesten identisk med den for beregning av statistiske begreper populasjon og prøve gjennomsnitt, med små variasjoner i variablene som brukes:
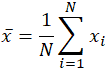
gjennomsnittet er ofte betegnet som x, uttalt «x bar», og selv i andre bruksområder når variabelen ikke er x, er barnotasjonen en vanlig indikator for noen form for gjennomsnitt. I det spesifikke tilfellet av populasjonsmiddel, i stedet for å bruke variabelen x, brukes det greske symbolet mu, eller μ. Tilsvarende, eller heller forvirrende, er prøvemiddelverdien i statistikk ofte indikert Med en kapital X. Gitt datasettet 10, 2, 38, 23, 38, 23, 21, bruk av summasjonen ovenfor gir:
|
10 + 2 + 38 + 23 + 38 + 23 + 21
|
= | = 22.143 |
som tidligere nevnt er dette en av de enkleste definisjonene av gjennomsnittet, og noen andre inkluderer det vektede aritmetiske gjennomsnittet (som bare adskiller seg ved at visse verdier i datasettet bidrar mer verdi enn andre) og geometrisk gjennomsnitt. Riktig forståelse av gitte situasjoner og sammenhenger kan ofte gi en person de verktøyene som er nødvendige for å bestemme hvilken statistisk relevant metode som skal brukes. Generelt bør gjennomsnitt, median, modus og rekkevidde ideelt sett alle beregnes og analyseres for et gitt utvalg eller datasett, siden de belyser ulike aspekter av de oppgitte dataene, og hvis de vurderes alene, kan det føre til feilrepresentasjoner av dataene, som det vil bli demonstrert i de følgende avsnittene.
Median
det statistiske konseptet med medianen er en verdi som deler en datautvalg, populasjon eller sannsynlighetsfordeling i to halvdeler. Å finne medianen innebærer i hovedsak å finne verdien i en dataprøve som har en fysisk plassering mellom resten av tallene. Merk at når du beregner medianen for en endelig liste over tall, er rekkefølgen av dataprøver viktig. Konvensjonelt er verdiene oppført i stigende rekkefølge, men det er ingen reell grunn til at oppføring av verdiene i synkende rekkefølge vil gi forskjellige resultater. I tilfelle hvor det totale antall verdier i en dataprøve er merkelig, er medianen bare tallet midt på listen over alle verdier. Når dataprøven inneholder et jevnt antall verdier, er medianen gjennomsnittet av de to mellomverdiene. Selv om dette kan være forvirrende, husk bare at selv om medianen noen ganger innebærer beregning av et gjennomsnitt, når dette tilfellet oppstår, vil det bare innebære de to mellomverdiene, mens et gjennomsnitt involverer alle verdiene i dataprøven. I odde tilfeller der det bare er to dataprøver eller det er et jevnt antall prøver der alle verdiene er de samme, vil gjennomsnittet og medianen være det samme. Gitt det samme datasettet som før, vil medianen bli anskaffet på følgende måte:
2,10,21,23,23,38,38
etter å ha notert dataene i stigende rekkefølge, og bestemt at det er et merkelig antall verdier, er det klart at 23 er medianen gitt denne saken. Hvis det var en annen verdi lagt til datasettet:
2,10,21,23,23,38,38,1027892
siden det er et jevnt antall verdier, vil medianen være gjennomsnittet av de to midterste tallene, i dette tilfellet 23 og 23, hvorav gjennomsnittet er 23. Legg merke til at i dette datasettet har tilsetningen av en outlier (en verdi godt utenfor det forventede verdiområdet), verdien 1,027,892, ingen reell effekt på datasettet. Hvis imidlertid gjennomsnittet beregnes for dette datasettet, er resultatet 128 505,875. Denne verdien er tydeligvis ikke en god representasjon av de syv andre verdiene i datasettet som er langt mindre og nærmere i verdi enn gjennomsnittet og outlier. Dette er hovedfordelen ved å bruke medianen til å beskrive statistiske data i forhold til gjennomsnittet. Mens både, så vel som andre statistiske verdier, skal beregnes når man beskriver data, hvis bare en kan brukes, kan medianen gi et bedre estimat av en typisk verdi i et gitt datasett når det er ekstremt store variasjoner mellom verdier.
Modus
i statistikk er modusen verdien i et datasett som har flest tilbakefall. Det er mulig for et datasett å være multimodalt, noe som betyr at det har mer enn en modus. For eksempel:
2,10,21,23,23,38,38
Både 23 og 38 vises to ganger hver, noe som gjør dem begge en modus for datasettet ovenfor.
på samme måte som gjennomsnitt og median, brukes modusen som en måte å uttrykke informasjon om tilfeldige variabler og populasjoner. I motsetning til middel og median er modusen imidlertid et konsept som kan brukes på ikke-numeriske verdier som merket av tortilla chips som oftest kjøpes fra en matbutikk. For eksempel, når man sammenligner merkene Tostitos, Mission og XOCHiTL, Hvis Det er funnet At I salg av tortilla chips, Er XOCHiTL modusen Og selger i et 3:2:1-forhold sammenlignet med Henholdsvis Tostitos og Mission brand tortilla chips, kan forholdet brukes til å bestemme hvor mange poser av hvert merke som skal lagres. I tilfelle hvor 24 poser med tortilla chips selge i løpet av en gitt periode, butikken ville lager 12 poser Med XOCHiTL chips, 8 Av Tostitos, og 4 Av Oppdrag hvis du bruker modus. Hvis butikken bare brukte et gjennomsnitt og solgte 8 poser av hver, kunne det potensielt miste 4 salg hvis en kunde bare ønsket XOCHiTL chips og ikke noe annet merke. Som det fremgår av dette eksemplet, er det viktig å ta hensyn til alle manerer av statistiske verdier når man forsøker å trekke konklusjoner om noen dataprøve.
Område
området for et datasett i statistikk er forskjellen mellom de største og de minste verdiene. Mens rekkevidde har forskjellige betydninger innenfor ulike områder av statistikk og matematikk, er dette den mest grunnleggende definisjonen, og er det som brukes av den medfølgende kalkulatoren. Bruker samme eksempel:
2,10,21,23,23,38,38
38 – 2 = 36
utvalget i dette eksemplet er 36. På samme måte som gjennomsnittet kan rekkevidden påvirkes betydelig av ekstremt store eller små verdier. Bruker samme eksempel som tidligere: