Overland flow (eller overflate avrenning) forekommer i to tilfeller:
1. når intensiteten av nedbør som når overflaten, overstiger infiltrasjonskapasiteten til jorda. Denne prosessen er kjent Som Hortonian overland flow.
2. når kombinasjonen av nedbørsintensitet og varighet (og oppstart fra høyere områder) metter jorda og øker vanntabellen til overflaten. Denne prosessen er kjent som metning overland flow.
Case-Studier: Nederland; Belgia; Spania; Kenya; Ghana, Kenya Og Mali
Se også:
- Synker
- Hortonisk og metning overlandstrøm (Infiltrasjon)
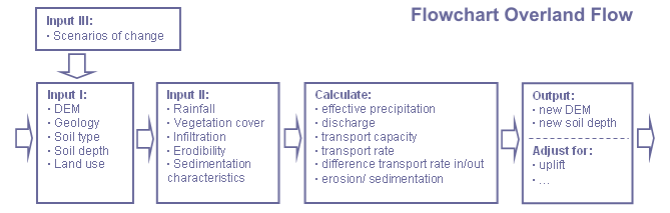
Teknisk Informasjon
vann erosjon og sedimenteringsmodul av modellen har to grunnleggende forutsetninger: 1) den potensielle energien i overflatevannstrømmen er drivkraften for sedimenttransport og 2) forskjellen mellom sedimentinngang og utgang av en gittercelle er lik nettoøkningen i lagring (kontinuitetsligning for sedimentbevegelse) (Schoorl et al., 2000). Prosessbeskrivelsen er avledet Fra Tidlige Verk Av Kirkby (Kirkby, 1971) Og Foster and Meyer (Foster and Meyer, 1972a; Foster and Meyer, 1972b), som bruker 2d formler for å beregne vann erosjon og sedimentering. FOR LAPSUS-modellen er formlene tilpasset for å kunne simulere romlig (3D)vann erosjon og sedimentering (Schoorl et al., 2000). Formlene som er omtalt nedenfor, er basert PÅ 2d-formlene Til Kirkby Og Foster Og Meyer og med de medfølgende enhetene (Foster Og Meyer, 1972a; Foster Og Meyer, 1972b; Kirkby, 1971).
etter beregning av utslipp Q sedimentet transportkapasitet C (m2 tid-1) i gittercellen kan beregnes som funksjon av utslipp og helling følgende:
(1.1) C = α * Qm * Λ
Der Λ er skråningsgradient ( – ) og m ( – ) og n ( – ) er konstanter som gir en indikasjon på systemet som studeres: m = 0 og n = 1 antyder jordkryp, mens m = n = 3 antyder store elver (Kirkby, 1971). Ingen strenge grenser kan gis da effekten av m og n avhenger av interaksjoner med andre modellparametere. Dummy variable α brukes til å korrigere enhetene.
sedimenttransporthastigheten S (m2 time-1) beregnes etter den integrerte kontinuitetsligningen for sedimentbevegelse (Ekv. 1.2 og 1.3). Sammensetningen av den brukte e-power termen i formelen avhenger av balansen mellom transporthastigheten av sediment allerede i transport s0 (m2 time-1) (innkommende sedimentfluss av alle høyere naboer i rutenettcellen) og sedimenttransportkapasitet C: hvis S0 < C erosjon resultater, mens Når S0 > C sedimentering resultater. Når rutenettet cellen er erodert følgende formel for sediment transporthastighet S brukes:
(1.2) S = C + (S0 – C) * e-dx * D / C
når sedimenter avsettes I gittercellen brukes følgende formel For sedimenttransporthastighet S:
(1.3) S = C + (S0 – C)·e-dx·T/C
hvorved transporthastigheten Av sediment s over gittercellestørrelse dx (m) beregnes ved å sammenligne sedimenttransportkapasitet C Med transporthastigheten av sediment allerede i transport S0 (m2 tid-1) minus sedimenttransportkapasitet C, redusert med en e-effekt som følge av gittercellestørrelse, løsningskapasitet D eller oppgjørskapasitet T og sedimenttransportkapasitet C.
Løsningskapasitet D (m tid-1), som representerer hvor lett sediment erodert av overflaten, beregnes som funksjon av utslipp og helling etter:
(1.4) D = Kes * Q * Λ
der Kes (m-1) er en klumpet overflatefaktor som indikerer overflatenes erodibilitet. Oppgjørskapasitet T (m tid-1), som representerer hvor lett sediment avsettes på overflaten, beregnes etter:
(1.5) D = Pes * Q * Λ
der Pes (m-1) er en overflatefaktor som indikerer klumpede sedimenteringsegenskaper.
ved å sammenligne sedimenttransporthastigheten S av gittercellen med sedimentet som allerede er i transport s0, kan endringen i sedimenttransporthastigheten dS, og dermed erosjon eller sedimentering, beregnes etter:
(1.6) dS = S-S0
dS kan omberegnes til erosjon eller sedimentering i meter ved å dele den med rutenettlengden dx (m) og multiplisere den med tidstrinnet (tid). Den resulterende verdien brukes til å korrigere den digitale høydemodellen og jorddybdekartet for følgende tidstrinn.
sammenligningen av e-power bestemmer hvor mye av forskjellen mellom transportkapasitet C og transport rate av sediment S kan være «fornøyd» i gittercellen. Avhengig av verdiene til de involverte variablene varierer resultatet av e-effekten mellom 0 og 1. I ekstreme situasjoner når dx og D/T kombinert er mye større Enn C, e-power nærmer seg null og transport rate av sediment S er lik sediment transportkapasitet C. deretter maksimal erosjon eller sedimentering er nådd. Men i den andre ytterligheten når dx og D/T kombinert er mye mindre Enn C, e-power nærmer seg 1 og transport rate av sedimenter S er lik transport rate av sedimenter allerede i transport s0 og ingen erosjon eller avsetning oppstår. I mindre ekstreme situasjoner modellen er sannsynlig å simulere sediment transporthastighet s nær transportkapasitet C. i tilfelle S0 > C mer sediment transporteres enn det som ville være tillatt basert på gittercellene ovenfor og mindre enn den maksimale sediment avsettes. E-power resulterer derfor i underkonsentrerte og superkonsentrerte strømmer i modellen, som utjevner erosjon og avsetning over skråningen. Åpenbart er utfallet av e-power-sammenligningen svært innflytelsesrik for erosjon og sedimentering. Sammenligning Av Eq. 1.1 og 1.4 / 1.5 det er klart at utslipp og helling er involvert i både transportkapasiteten C og i beregningene Av løsningskapasitet D Eller oppgjørskapasitet T. Dette betyr at i en situasjon når m = n = 1, reduseres termen i e-kraften til dx * Kes eller dx * Pes. Ettersom gittercellestørrelsen er en konstant verdi, Erodibility Kes og sedimenterbarhet Pes de viktigste variablene i en situasjon med lave m-og n-verdier. Når m og n er større, øker effekten av transportkapasiteten C på e-effektperioden. Utfallet av e-power sikt er i den situasjonen vanskeligere å forutsi.