Jeśli naszym celem jest znalezienie relatywistycznego uogólnienia równania Poissona dla pola grawitacyjnego:
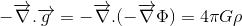
gdzie Φ odnosi się do potencjału grawitacyjnego, a ρ do gęstości masy, jesteśmy w połowie drogi.
rzeczywiście, widzieliśmy już w naszym poprzednim artykule tensor energia-pęd, że uogólnienie gęstości masy (prawe określenie równania) odpowiada energii-pęd Tµv.
wydaje się więc rozsądne założenie, że nasze równanie powinno mieć postać:
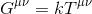
gdzie k oznacza Skalar, a Gµv, zwany tensorem Einsteina reprezentuje tensor Rangi-2 opisujący krzywiznę czasoprzestrzeni .
o ile nam wiadomo, Gµv powinien przestrzegać następujących ograniczeń:
– powinna być zerowa w płaskiej czasoprzestrzeni
– powinna opisywać krzywiznę czasoprzestrzeni i być liniowa względem tensora Riemanna
– powinna być symetryczna i rzędu 2 (jako Tµv)
– powinna mieć zerową rozbieżność (jako Tµv)
– i wreszcie, w granice newtonowskie, powinno zmniejszyć się do 4ngp
pierwsza próba z tensorem Ricciego jako rozwiązaniem
przypominamy z naszego artykułu równanie geodezyjne granicy newtonowskiej, że potencjał grawitacyjny φ jest połączony z 00-składową metryki poprzez H00=(G00-1)/C2
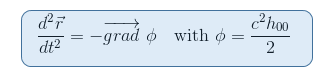
wydaje się więc naturalne szukanie tensora, który wiąże się z drugą pochodną metryki, co ma miejsce w przypadku tensora Riemanna. Ponadto Tensor Riemanna jest jedynym znanym nam do tej pory kandydatem do opisania krzywizny czasoprzestrzeni (por. drugie ograniczenie powyżej).
ponieważ musimy znaleźć tensor stopnia-2 i jeśli założymy, że musimy znaleźć rozwiązanie wyłącznie w kategoriach tensora Riemanna, wydaje się naturalne, aby najpierw rozważyć zakontraktowaną postać tensora Riemanna, znanego jako Tensor Ricciego.
aby to zobaczyć, przypomnijmy sobie wyrażenie tensora Riemanna z artykułu tensor krzywizny Riemanna Część II: wyprowadzenie z odchylenia geodezyjnego
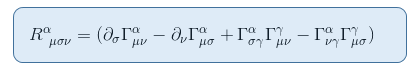
w granicach statycznego i słabego pola grawitacyjnego tylko jeden termin przyczynia się do R00:
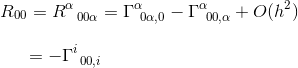
w tym samym artykule obliczyliśmy Ten symbol Christoffela i stwierdziliśmy, że
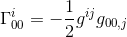
z przybliżeniem gij = nij i goo, j = hoo, j (patrz artykuł) otrzymujemy:
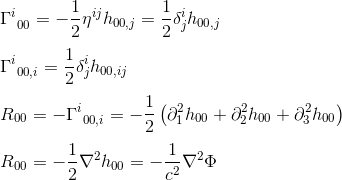
identyfikacja R00 z ΔΦ (operatorem Laplacjańskim) sugeruje, że równanie pola w ogólnej teorii względności powinno być równe stałej wielokrotności Tab.
w 1915 roku, używając tego równania, Einstein był nawet w stanie rozwiązać długotrwały problem precesji Peryhelium Merkurego, powodując napisanie w listopadzie tego roku, że „przez kilka dni byłem obok siebie z radosnym podnieceniem.”
ostatecznie Einstein musiał odrzucić tę pierwszą próbę, ze względu na fakt, że ogólna rozbieżność Rab nie unieważnia.
druga próba
istnieje tensor ściśle związany ze skalarem Ricciego, który można umieścić po lewej stronie bez sprzeczności. Daje to Tensor Einsteina zdefiniowany następująco:
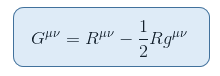
gdzie R = Raa jest skalarem Ricciego lub krzywizną skalarną.
ta forma Gab jest symetryczna i Rangi-2 i oczywiście opisuje krzywiznę czasoprzestrzeni. Więc pozostaje tylko pokazać, że całkowita pochodna wynosi zero
aby to zrobić, zaczynamy od tożsamości Bianchiego
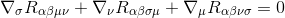
mnożąc przez gγσgαμgβν (pochodne metryki są zerowe, więc działają jako stałe i mogą być wzięte wewnątrz pochodnych), daje się do:
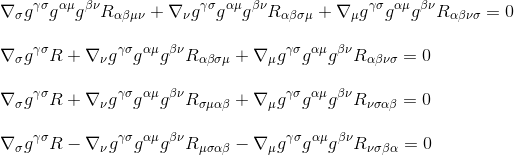
stosując definicję tensora Ricciego Rµv=gμβgνσRβσ (Krok 3) i zmieniając nazwy indeksów (Krok 4) otrzymujemy
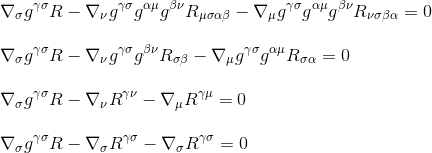
faktoryzując pochodną otrzymujemy w końcu
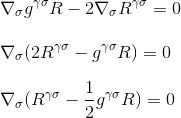
co dokładnie chcieliśmy wykazać: dywergencja tensora Einsteina jest równa null, i znaleźliśmy prawy kandydat dla lewej strony naszego równania krzywizna / masa-energia.