por favor, forneça números separados por vírgula para calcular.
as Estatísticas Relacionadas a Calculadora | Desvio Padrão da Calculadora | Tamanho da Amostra Calculadora
Média
A palavra significa, que é um homônimo para várias outras palavras no idioma inglês, é igualmente ambígua, mesmo na área de matemática. Dependendo do contexto, seja matemático ou estatístico, o que significa a “média” muda. Em sua definição matemática mais simples sobre conjuntos de dados, a média utilizada é a média aritmética, também referida como expectativa matemática, ou média. Desta forma, a média refere-se a um valor intermediário entre um conjunto discreto de números, ou seja, a soma de todos os valores do conjunto de dados, dividido pelo número total de valores. A equação para calcular uma média aritmética é virtualmente idêntica à do cálculo dos conceitos estatísticos da população e da média amostral, com ligeiras variações nas variáveis utilizadas. :
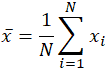
a média é muitas vezes denotada como x, pronunciado “x bar”, e mesmo em outros usos quando a variável não é x, a notação de bar é um indicador comum de alguma forma de média. No caso específico da população significa, ao invés de usar a variável x, o símbolo grego mu, ou μ, É usado. Da mesma forma, ou melhor, confusamente, a média da amostra em estatísticas é frequentemente indicada com um x maiúsculo. Dado o conjunto de Dados 10, 2, 38, 23, 38, 23, 21, aplicação da soma acima dos rendimentos:
|
10 + 2 + 38 + 23 + 38 + 23 + 21
|
= | = 22.143 |
Como mencionado anteriormente, essa é uma das mais simples definições da média, e alguns outros incluem a média aritmética ponderada (que só difere na medida em que certos valores no conjunto de dados contribuir mais valor do que outros), e a média geométrica. Uma compreensão adequada de situações e contextos determinados pode muitas vezes fornecer a uma pessoa as ferramentas necessárias para determinar que método estatisticamente relevante usar. Em geral, a média, a mediana, o modo e a gama devem idealmente ser todos calculados e analisados para uma dada amostra ou conjunto de dados, uma vez que elucidam diferentes aspectos dos dados em questão, e se considerados isoladamente, podem levar a deturpações dos dados, como será demonstrado nas secções seguintes.
mediana
o conceito estatístico da mediana é um valor que divide uma amostra de dados, população ou distribuição de probabilidade em duas metades. Encontrar a mediana envolve essencialmente encontrar o valor numa amostra de dados que tem uma localização física entre o resto dos números. Note que ao calcular a mediana de uma lista finita de números, a ordem das amostras de dados é importante. Convencionalmente, os valores são listados em ordem ascendente, mas não há nenhuma razão real para que listar os valores em ordem descendente forneça resultados diferentes. No caso em que o número total de valores numa amostra de dados é ímpar, a mediana é simplesmente o número no meio da lista de todos os valores. Quando a amostra de dados contém um número par de valores, a mediana é a média dos dois valores médios. Embora isso possa ser confuso, basta lembrar que, embora a mediana às vezes envolva a computação de uma média, quando este caso surge, ela envolverá apenas os dois valores médios, enquanto uma média envolve todos os valores na amostra de dados. Nos casos ímpares em que existam apenas duas amostras de dados ou em que exista um número par de amostras em que todos os valores sejam os mesmos, a média e a mediana serão as mesmas. Dado o mesmo conjunto de dados, como antes, a mediana seria adquirido da seguinte forma:
2,10,21,23,23,38,38
Depois de listar os dados em ordem crescente, e a determinação de que há um número ímpar de valores, é claro que 23 é a mediana dado a este caso. Se houvesse outro valor acrescentado ao conjunto de dados:
2,10,21,23,23,38,38,1027892
uma vez que há um número par de valores, a mediana será a média dos dois números meio, neste caso, 23 e 23, a média do que é 23. Note – se que neste conjunto de dados específico, a adição de um valor fora do intervalo de valores esperado, o valor 1,027,892, não tem efeito real sobre o conjunto de dados. Se, no entanto, a média for calculada para este conjunto de dados, o resultado é 128,505.875. Este valor não é claramente uma boa representação dos outros sete valores no conjunto de dados que são muito menores e mais próximos em valor do que a média e o outlier. Esta é a principal vantagem de utilizar a mediana na descrição dos dados estatísticos em comparação com a média. Enquanto ambos, bem como outros valores estatísticos, deve ser calculado ao se descrever dados, se apenas um pode ser usado, a mediana pode fornecer uma melhor estimativa de um valor típico em um determinado conjunto de dados, quando não são muito grandes variações entre os valores.
modo
nas estatísticas, o modo é o valor num conjunto de dados que tem o maior número de recorrências. É possível que um conjunto de dados seja multimodal, o que significa que tem mais de um modo. Por exemplo:
2,10,21,23,23,38,38
ambos 23 e 38 aparecem duas vezes cada, tornando-os um modo para o conjunto de dados acima.
similarmente à média e mediana, o modo é usado como uma forma de expressar informações sobre variáveis aleatórias e populações. Ao contrário da média e mediana, no entanto, o modo é um conceito que pode ser aplicado a valores não-numéricos, como a marca de chips tortilla mais comumente comprado de uma mercearia. Por exemplo, quando se comparam as marcas Tostitos, Missão e XOCHiTL, se se verificar que na venda de batatas fritas, XOCHiTL é o modo e vende em uma relação de 3:2:1 em relação a Tostitos e a Missão da marca tortilla chips, respectivamente, a relação poderia ser usado para determinar quantos sacos de cada marca para o estoque. No caso em que 24 sacos de tortilla chips vendem durante um determinado período, a loja armazenaria 12 sacos de Xochitl chips, 8 de Tostitos, e 4 de missão se usando o modo. Se, no entanto, a loja simplesmente usou uma média e vendeu 8 sacos de cada, Ele poderia potencialmente perder 4 vendas se um cliente desejava apenas chips XOCHiTL e não qualquer outra marca. Como é evidente a partir deste exemplo, é importante ter em conta todas as maneiras dos valores estatísticos ao tentar tirar conclusões sobre qualquer amostra de dados.
Range
the range of a data set in statistics is the difference between the largest and the smallest values. Enquanto o intervalo tem significados diferentes dentro de diferentes áreas de estatística e matemática, esta é a sua definição mais básica, e é o que é usado pela calculadora fornecida. Usando o mesmo exemplo:
2,10,21,23,23,38,38
38 – 2 = 36
o intervalo neste exemplo é 36. Da mesma forma que a média, o intervalo pode ser significativamente afetado por valores extremamente grandes ou pequenos. Usando o mesmo exemplo que anteriormente: