















@brandonskerritt51brandon
Escritor 👽

Timsort: a very fast , O(n log n), stable sorting algorithm built for the real world — not constructed in academia.
Clique aqui para exibir o artigo atualizado:

Timsort é um algoritmo de ordenação, que é eficiente para os dados do mundo real e não criados em um laboratório acadêmico. Tim Peters criou o Timsort para a linguagem de programação Python em 2001. Timsort primeiro analisa a lista que está tentando classificar e, em seguida, escolhe uma abordagem baseada na análise da lista.
desde que o algoritmo foi inventado tem sido usado como o algoritmo de ordenação padrão em Python, Java, a plataforma Android, e na GNU Octave.
Timsort’s big o notation is o(n log n). Para aprender sobre a notação Big O, leia isto.

Timsort de ordenação do tempo é o mesmo que Mergesort, que é mais rápido do que a maioria dos outros tipos que você pode saber. Timsort realmente faz uso do tipo de inserção e mescla, como você verá em breve.
Peters projetou Timsort para usar elementos já ordenados que existem na maioria dos conjuntos de dados do mundo real. Ele chama esses elementos já ordenados de “corridas naturais”. Itera sobre os dados que coletam os elementos em runs e simultaneamente fundem esses runs juntos em um.
a matriz tem menos de 64 elementos nela
se a matriz que estamos tentando classificar tem menos de 64 elementos nela, Timsort irá executar uma ordenação de inserção.
uma ordenação de inserção é uma ordenação simples que é mais eficaz em pequenas listas. É bastante lento em listas maiores, mas muito rápido com listas pequenas. A idéia de uma inserção de classificação é a seguinte:
- Olhar elementos, um por um
- Construir lista ordenada por inserir o elemento no local correto
Aqui está uma tabela de rastreamento mostrando como a inserção de classificação seria classificar a lista

neste caso estamos inserindo os elementos recém-ordenados em um novo sub-array, que começa no início do array.
Aqui está um gif mostrando a inserção de classificação:
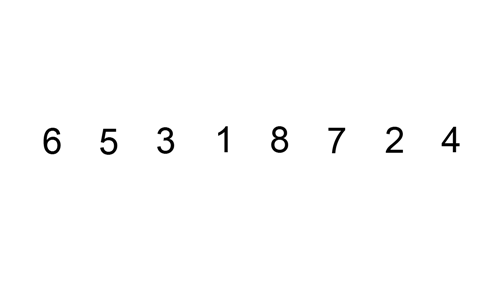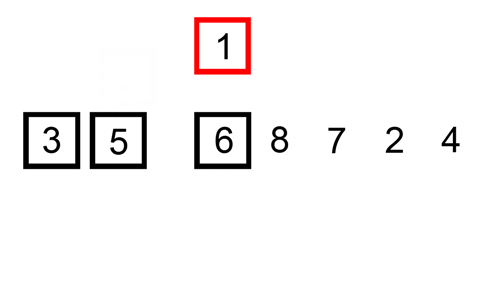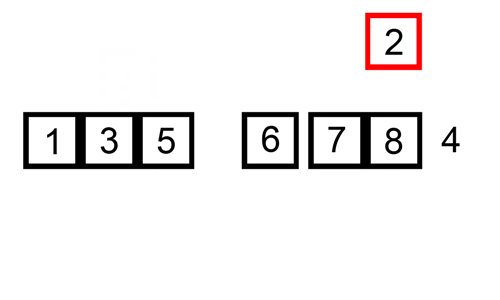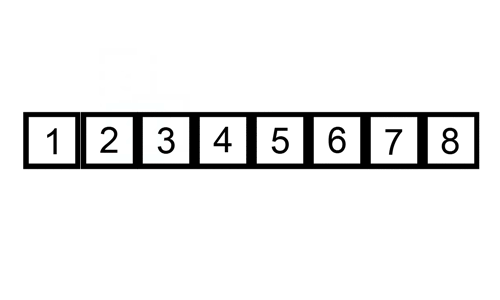
Mais sobre executa
Se a lista for maior do que 64 elementos que o algoritmo vai fazer uma primeira passagem pela lista à procura de peças que são estritamente crescente ou decrescente. Se a parte está a diminuir, vai reverter essa parte.
por isso, se a corrida está a diminuir, vai parecer-se com isto (onde a corrida está a negrito):

se não diminuir, ficará assim:

the minrun is a size which is determined based on the size of the array. O algoritmo seleciona – o de modo que a maioria dos runs em um array Aleatório são, ou se tornam minrun, em comprimento. Funding 2 arrays é mais eficiente quando o número de Corridas é igual ou ligeiramente inferior a uma potência de dois. Timsort escolhe minrun para tentar garantir essa eficiência, certificando-se de que minrun é igual ou inferior a um poder de dois.
o algoritmo escolhe minrun da Gama 32 a 64 inclusive. Ele escolhe minrun de tal forma que o comprimento da matriz original, quando dividido por minrun, é igual ou ligeiramente inferior a uma potência de dois.
se o comprimento da corrida for inferior a minrun, você calcula o comprimento dessa corrida longe de minrun. Usando este novo número, você pega que muitos itens antes da execução e executar um tipo de inserção para criar uma nova execução.
então se minrun é 63 e o comprimento da corrida é 33, você faz 63-33 = 30. Você, em seguida, pegar 30 elementos na frente do final da execução, então este é 30 itens da execução e, em seguida, realizar um tipo de inserção para criar uma nova execução.
depois desta parte ter terminado devemos agora ter um monte de séries ordenadas em uma lista.
Fundir

Timsort agora executa mergesort para mesclar as corridas juntos. No entanto, a Timsort assegura-se de manter a estabilidade e fundir o equilíbrio durante a ordenação da junção.
para manter a estabilidade não devemos trocar 2 números de igual valor. Isso não só mantém suas posições originais na lista, mas permite que o algoritmo seja mais rápido. Em breve discutiremos o equilíbrio da fusão.
à medida que a Timsort encontra corridas, Adiciona-as a uma pilha. Uma simples pilha ficaria assim:

Imagine uma pilha de placas. Você não pode tirar pratos do fundo, então você tem que levá-los do topo. O mesmo é verdade sobre uma pilha.
Timsort tenta equilibrar duas necessidades concorrentes quando a fusão acontece. Por um lado, gostaríamos de adiar a fusão o mais tempo possível, a fim de explorar padrões que possam surgir mais tarde. Mas gostaríamos ainda mais de fazer a fusão o mais rápido possível para explorar a execução que a execução acaba de ser encontrada ainda é alta na hierarquia de memória. Também não podemos atrasar a fusão de “muito tempo” porque consome memória para lembrar as corridas que ainda estão por montar, e a pilha tem um tamanho fixo.
para garantir que temos este compromisso, Timsort mantém o controle dos três itens mais recentes na pilha e cria duas leis que devem ser verdadeiras desses itens:
1. A > B + C
2. B > c
onde A, B E C são os três itens mais recentes na pilha.Nas palavras do próprio Tim Peters:
o Que acabou por ser um bom compromisso mantém duas constantes na pilha entradas, onde A, B e C são os comprimentos dos três righmost ainda não mesclada fatias
Normalmente, a fusão de execuções adjacentes de diferentes comprimentos no local é difícil. O que torna ainda mais difícil é Termos de manter a estabilidade. Para contornar isso, Timsort deixa de lado a memória temporária. Ele coloca o menor (chamando ambos corre A E B) dos dois corre para essa memória temporária.
Galope

Enquanto Timsort é a fusão de A e B, ele percebe que uma corrida tem sido a “ganhar” muitas vezes em uma linha. Se ele acabou que a execução a consistia de números inteiramente menores do que a execução B, em seguida, a execução A acabaria de volta em seu lugar original. Fundir as duas corridas envolveria muito trabalho para não conseguir nada.
mais frequentemente do que não, os dados terão alguma estrutura interna pré-existente. Timsort assume que se um monte de executar Um dos valores são inferiores a B valores, então é provável que Um vai continuar a ter valores menores do que B.
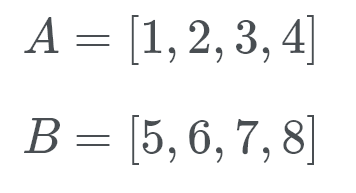
Timsort irá então entrar no modo galopante. Em vez de verificar A e B uns contra os outros, a Timsort realiza uma busca binária para a posição apropriada de b em A. desta forma, a Timsort pode mover uma seção inteira de A para o lugar. Em seguida, Timsort procura a localização apropriada de A Em B. Timsort irá então mover uma seção inteira da lata B de uma vez, e para o lugar.Vamos ver isto em acção. Timsort verificações de B (que é 5) e usando uma pesquisa binária olha para o local correto em A.
Bem, B pertence na parte de trás da lista de A. Agora Timsort verifica a existência de Uma (que é 1) no local correto do B. Então nós estamos olhando para ver onde o número 1 vai. Este número vai para o início do B. Agora sabemos que o B pertence ao fim do A e do A ao início do B.
acontece que esta operação não vale a pena se o local apropriado para B é muito perto do início de A (ou vice-versa). então o modo de galope sai rapidamente se não estiver a compensar. Além disso, Timsort toma nota e torna mais difícil entrar no modo gallop mais tarde, aumentando o número de vitórias consecutivas A-only ou B-only necessárias para entrar. Se o modo gallop está a dar resultado, o Timsort torna mais fácil reentrar.Em resumo, Timsort faz 2 coisas incrivelmente bem:
- Ótimo desempenho em matrizes com preexistente estrutura interna
- Ser capaz de manter um quadro estável de classificação
Anteriormente, a fim de alcançar uma estável de classificação, o que você teria para o zip itens na sua lista para cima com números inteiros, e classificá-lo como um conjunto de tuplas.
Código
se não estiver interessado no código, não hesite em saltar esta parte. Há mais informações abaixo desta secção.
o código fonte abaixo é baseado no trabalho de Nanda Javarma. O código fonte não está completo, nem é semelhante ao código fonte offical tried() do Python. Este é apenas um Timsort estúpido que implementei para ter uma sensação geral de Timsort. Se você quiser ver o código fonte original de Timsort em toda a sua glória, confira aqui. Timsort é oficialmente implementado em C, não em Python.
Timsort é realmente construído em Python, então este código apenas serve como um explicador. Para usar o Timsort basta escrever:
list.sort()
Ou
sorted(list)
Se você deseja dominar como Timsort obras e começar uma sensação para ela, eu sugiro que você tente implementá-lo!Este artigo é baseado na introdução original de Tim Peters à Timsort, encontrada aqui.Gostou deste artigo? Conecte-se comigo nas redes sociais para discutir todas as coisas relacionadas com ciência da computação 😁