Arealmoment af inerti-typisk tværsnit i

Arealmoment af inerti eller inertimoment for et område – også kendt som andet øjeblik af område – i, er en formegenskab, der bruges til at forudsige afbøjning, bøjning og stress i bjælker.

Arealmoment for inerti – kejserlige enheder

• inches4

Arealmoment for inerti – metriske enheder

• mm4
• cm4
• m4

konvertering mellem enheder

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4, 16h105 mm4 = 41.6 cm4

eksempel – Konverter mellem Arealmoment af inerti enheder

9240 cm4 kan konverteres til mm4 ved at multiplicere med 104

(9240 cm4) 104 = 9.24 107 mm4

Træghedsmoment (Træghedsmoment for et område eller andet område)

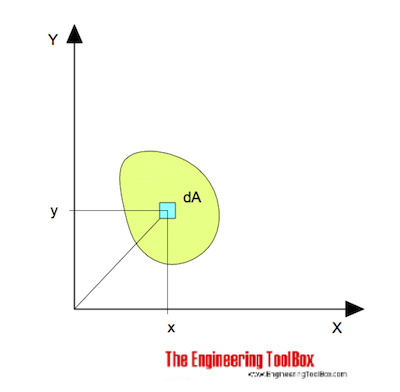
til bøjning omkring h – aksen kan udtrykkes som

ik = lit Y2 dA (1)

hvor

ik = arealets inertimoment relateret til H-aksen (m4, mm4, inches4)

y = arealets inertimoment relateret til H-aksen (m4, mm4, inches4)

y = arealets inertimoment relateret til H-aksen (m4, mm4, inches4)

y = vinkelret afstand fra aksen til elementet da (M, mm, tommer)

dA = et elementært område (m2, mm2, tommer2)

inertimomentet til bøjning omkring Y – aksen kan udtrykkes som

Iy = 2 da (2)

hvor

Iy = Arealmoment for inerti relateret til y-aksen (m4, mm4, inches4)

h = den vinkelrette afstand fra akse y til elementet dA (m, mm, tommer)

Arealmoment for typisk tværsnit i

• arealets inertimoment for typiske tværsnit II

fast kvadratisk tværsnit

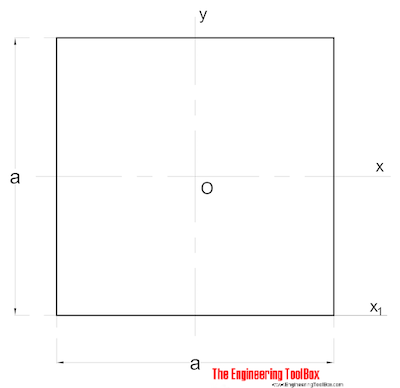
arealets inertimoment for en fast kvadratisk sektion kan beregnes som

ik = a4 / 12 (2)

hvor

a = side (mm, m, in..)

IY = a4 / 12 (2B)

fast rektangulært tværsnit

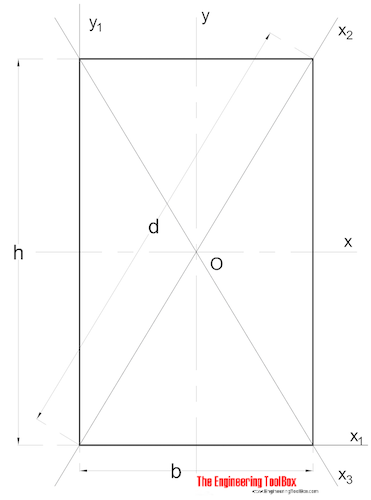
Arealmomentet for ineria for en rektangulær sektion kan beregnes som

ik = b h3 / 12 (3)

hvor

b = bredde

h = højde

IY = b3 h / 12 (3b)

fast cirkulært tværsnit

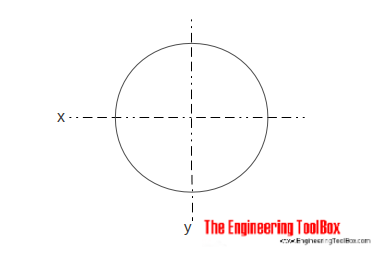
arealets inertimoment for et fast cylindrisk afsnit kan beregnes som

ik = lk r4 /4

= D4 / 64 (4)

hvor

r = radius

d = diameter

Iy = KR4 / 4

= KR4 / 64 (4b)

hul cylindrisk tværsnit

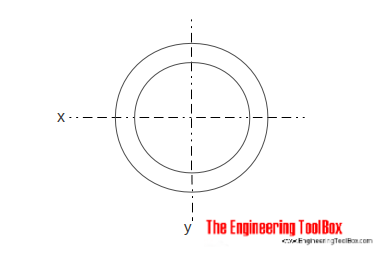
Arealmomentet for en hul cylindrisk sektion kan beregnes som

kr = KR4 (do4-di4) / 64 (5)

hvor

do = cylinder udvendig diameter

di = cylinder indvendig diameter

IY = venstre (do4-di4) / 64 (5b)

firkantet sektion – Diagonale øjeblikke

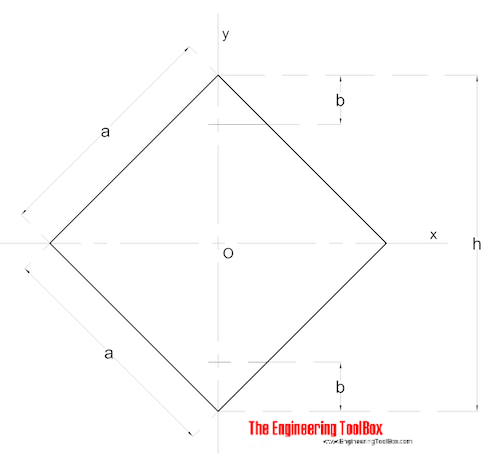
de diagonale Arealmomenter af inerti for en firkantet sektion kan beregnes som

/ 12 (6)

rektangulær sektion-område øjeblikke på enhver linje gennem tyngdepunktet

rektangulær sektion og område af øjeblik på linje gennem tyngdepunktet kan beregnes som

ik = (b h / 12) (h2 cos2 A + b2 sin2 a) (7)

symmetrisk form

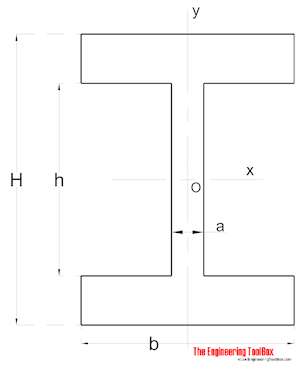
arealets inertimoment for en symmetrisk formet sektion kan beregnes som

ik = (a h3 / 12) + (b / 12) (H3-h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

ikke – symmetrisk form

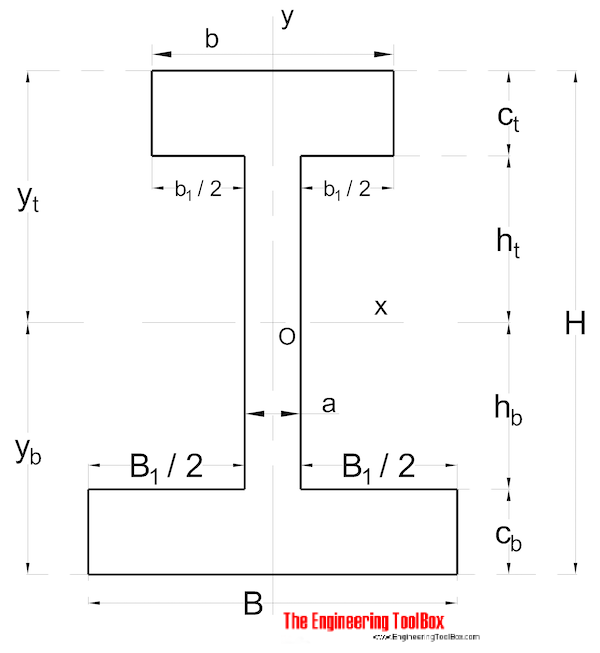
arealets inertimoment for en ikke-symmetrisk formet sektion kan beregnes som

IK = (1 / 3) (B YB3-B1 HB3 + B YT3-B1 HT3) (9)

• arealets inertimoment for typiske tværsnit II

arealets inertimoment vs. polært inertimoment vs. Moment af inerti

• “arealets inertimoment”er en formegenskab, der bruges til at forudsige afbøjning, bøjning og spænding i bjælker
• ” polært inertimoment”som et mål for en stråles evne til at modstå vridning – hvilket er nødvendigt for at beregne vridningen af en stråle, der udsættes for drejningsmoment
• ” inertimoment ” er et mål for et objekts modstand mod ændring i rotationsretning.

sektionsmodul

• “Sektionsmodulet” er defineret som V = I / y, hvor jeg er arealets inertimoment og y er afstanden fra den neutrale akse til en given fiber