hvis vores mål er at finde den relativistiske generalisering af Poisson ‘ s ligning for gravitationsfeltet:
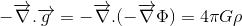
hvor der henvises til gravitationspotentialet og til massetætheden, er vi halvvejs.
faktisk har vi allerede set i vores tidligere artikel energi-momentum tensor, at generaliseringen af massetætheden (højre hånd sigt af ligningen) svarer til energi-momentum t-Krishv.
det forekommer rimeligt at antage, at vores ligning skal tage form af:
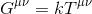
hvor k står for en skalar og G-Krustv, kaldet Einstein tensor repræsenterer en rang-2 tensor, der beskriver rumtids krumning .
så vidt vi ved, skal G Kurstv overholde følgende begrænsninger:
– det skal ophæve i flad rumtid
– det skal beskrive rumtidsrummets krumning og være lineær med hensyn til Riemann tensor
– det skal være symmetrisk og af rang 2 (som T – Kristiv)
– det skal have en null-divergens (som T-Kristiv)
– og endelig, I til 4ngp
første forsøg med Ricci tensor som løsning
vi husker fra vores artikel den geodesiske ligning i den nytoniske grænse, at gravitationspotentialet er forbundet med 00-komponenten i metrikken via H00=(G00-1)/C2
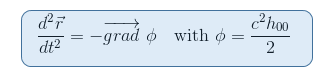
det forekommer så naturligt at kigge efter en tensor, der involverer den anden derivater af metricen, hvilket er tilfældet for Riemann tensor. Endvidere er Riemann tensor den eneste kandidat, som vi hidtil kender til at kunne beskrive rumtidskurvaturen (jf.anden begrænsning ovenfor).
da vi er nødt til at finde en rang-2 tensor, og hvis vi antager, at vi er nødt til at finde en løsning udelukkende med hensyn til Riemann tensor, synes det naturligt først at overveje den kontraherede form for Riemann tensor, kendt som Ricci tensor.
for at se dette, lad os huske udtrykket af Riemann tensor fra Tha artikel Riemann curvature tensor del II: afledning fra den geodesiske afvigelse
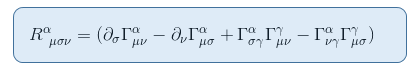
i grænsen for et statisk og svagt tyngdefelt bidrager kun et udtryk til R00:
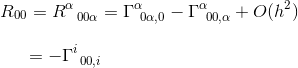
i samme artikel har vi beregnet dette Christoffel symbol og fundet det
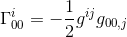
med tilnærmelsen af gij = nij og goo,J = hoo, j (se artiklen) får vi:
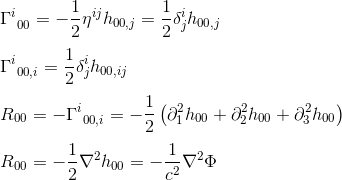
identifikationen af R00 med Kurt (Laplacian operator) antyder, at feltligningen i generel relativitet skal svare til Rab til et konstant multiplum af tab.
i 1915, ved hjælp af denne ligning, var Einstein endda i stand til at løse det langvarige problem med Mercury perihelion-præcession, hvilket fik til at skrive i November samme år, at “i et par dage var jeg ved siden af mig selv med glædelig spænding.”
til sidst måtte Einstein afvise dette første forsøg på grund af det faktum, at generelt divergens af Rab ikke ophæver.
andet forsøg
der er tensor tæt beslægtet med Ricci skalar, der kan sættes på venstre side uden Modsigelse. Dette giver Einstein tensor defineret som følger:
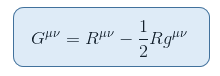
hvor R = Raa er Ricci skalar eller skalar krumning.
denne form for Gab er symmetrisk og af rang-2 og beskriver naturligvis rumtids krumning. Så det er bare at vise, at det samlede derivat er nul
for at gøre dette starter vi med Bianchi-identiteten
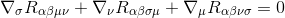
multiplicere igennem med G-kurg-kurg-kur (metrikderivaterne er nul, så de fungerer som konstanter og kan tages inde i derivaterne), det giver til:
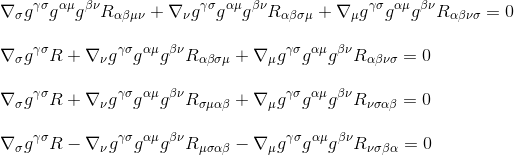
ved at bruge Ricci tensordefinitionen r Kristiv=g kristir kristir kristir (trin 3) og ved at omdøbe indekserne (trin 4) får vi
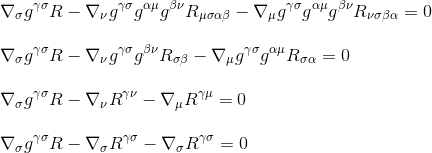
ved at faktorisere derivatet opnår vi endelig
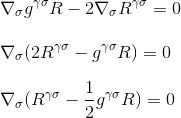
hvilket er præcis, hvad vi ønskede at demonstrere: divergensen af Einstein tensor er null, og vi har fundet den rigtige kandidat til venstre side af vores krumning/masse-energi ligning.