Logaritmer: Introduktion til “forholdet”

gå tilbage til Lektionsindekset | gør lektionerne i rækkefølge | Printvenlig side

logaritmer: Introduktion til
“forholdet” (side 1 af 3)

sektioner: Introduktion til logfiler, forenkling af logudtryk, almindelige og naturlige logfiler

logaritmer er det “modsatte” af eksponentialer, ligesom subtraktion er det modsatte af Tilføjelse og division er det modsatte af multiplikation. Logs” Fortryd ” eksponentialer. Teknisk set er logfiler inverserne af eksponentialer.

i praksis har jeg fundet det nyttigt at tænke på logfiler med hensyn til forholdet:

på venstre side ovenfor er den eksponentielle sætning “y = BKS”. På højre side ovenfor er “logb(y) = h” den ækvivalente logaritmiske sætning, der udtales” log-base-b af y er lig med H”; værdien af det underskrevne” b “er” logaritmens base”, ligesom b er basen i det eksponentielle udtryk”B”. Og ligesom basen b i en eksponentiel altid er positiv og ikke lig med 1, så er også basen b for en logaritme altid positiv og ikke lig med 1. Uanset hvad der er inde i logaritmen kaldes logens “argument”. Bemærk, at basen i både den eksponentielle ligning og logligningen (ovenfor) er “b”, men at h og y skifter sider, når du skifter mellem de to ligninger.

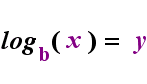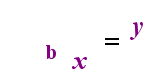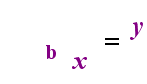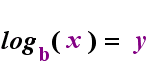
hvis du kan huske dette forhold (at uanset hvad der havde været logens argument bliver “ligeværdige” og hvad der havde været “ligeværdige” bliver eksponenten i eksponentiel og omvendt), så skulle du ikke have for mange problemer med logaritmer.

(jeg opfandt udtrykket “forholdet” selv. Du finder det ikke i din tekst, og dine lærere og vejledere aner ikke, hvad du taler om, hvis du nævner det for dem. “Forholdet” er helt ikke-standard terminologi. Hvorfor bruger jeg det alligevel? Fordi det virker.)

forresten: hvis du bemærkede, at jeg skiftede variablerne mellem de to bokse, der viste “forholdet”, har du et skarpt øje. Jeg gjorde det med vilje for at understrege, at pointen ikke er variablerne selv, men hvordan de bevæger sig.

• konverter “63 = 216” til det tilsvarende logaritmiske udtryk.

for at konvertere forbliver basen (det vil sige 6) den samme, men 3 og 216 skifter sider. Dette giver mig:

log6 (216) = 3 Copyright Peter Elisabeth Stapel 2002-2011 Alle rettigheder forbeholdes

• konverter “log4 (1024) = 5” til det tilsvarende eksponentielle udtryk.

for at konvertere forbliver basen (det vil sige 4) den samme, men 1024 og 5 skifter sider. Dette giver mig:

45 = 1024

Top| 1 | 2 | 3 | tilbage til indeks næste >>