Logaritmos: Introducción a «La Relación»

Volver al Índice de Lecciones | Hacer las Lecciones en Orden / Página para imprimir

Logaritmos: Introducción a
«La relación» (página 1 de 3)

Secciones: Introducción a los registros, Simplificando las expresiones de registro, Registros comunes y naturales

Los logaritmos son el «opuesto» de los exponenciales, así como la resta es lo opuesto a la suma y la división es lo opuesto a la multiplicación. Registros de exponenciales «deshacer». Técnicamente hablando, los registros son los inversos de los exponenciales.

En términos prácticos, he encontrado que es útil pensar en los registros en los términos de La Relación:

En el lado izquierdo de arriba es la exponencial de la declaración «y = bx». En el lado derecho de arriba, «logb(y) = x» es la sentencia logarítmica equivalente, que se pronuncia «log-base-b de y es igual a x»; El valor de la subíndice » b «es» la base del logaritmo», al igual que b es la base en la expresión exponencial»bx». Y, así como la base b en un exponencial es siempre positiva y no igual a 1, así también la base b para un logaritmo es siempre positiva y no igual a 1. Lo que está dentro del logaritmo se llama el «argumento» del registro. Tenga en cuenta que la base tanto en la ecuación exponencial como en la ecuación logarítmica (arriba) es «b», pero que la x y la y cambian de lado cuando cambia entre las dos ecuaciones.

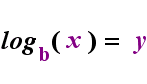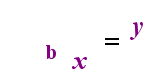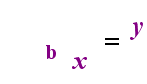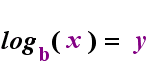
Si puedes recordar esta relación (que lo que haya sido el argumento del registro se convierte en» iguales «y lo que haya sido» iguales » se convierte en el exponente en el exponencial, y viceversa), entonces no deberías tener demasiados problemas con los logaritmos.

(Yo mismo acuñé el término «La Relación». No lo encontrarás en tu texto, y tus profesores y tutores no tendrán idea de lo que estás hablando si se lo mencionas. «La relación» es una terminología totalmente atípica. ¿Por qué lo uso de todos modos? Porque funciona.)

Por cierto: Si notaste que cambié las variables entre las dos cajas que muestran «La relación», tienes un ojo agudo. Lo hice a propósito, para enfatizar que el punto no son las variables en sí, sino cómo se mueven.

• Convierta «63 = 216» a la expresión logarítmica equivalente.

Para convertir, la base (es decir, el 6)sigue siendo la misma, pero el 3 y el 216 cambian de lado. Esto me da:

log6(216) = 3 Copyright © Elizabeth Stapel 2002-2011 Todos los derechos reservados

• Convierta «log4(1024) = 5» a la expresión exponencial equivalente.

Para convertir, la base (es decir, el 4) sigue siendo la misma, pero el 1024 y el 5 cambian de lado. Esto me da:

45 = 1024

Top| 1 | 2 | 3 | Volver a Índice Siguiente >>