
















Timsort: Un algoritmo de clasificación estable , O(n log n) muy rápido creado para el mundo real, no construido en el mundo académico.
Haga clic aquí para ver el artículo actualizado:

Timsort es un algoritmo de clasificación que es eficiente para datos del mundo real y no creado en un laboratorio académico. Tim Peters creó Timsort para el lenguaje de programación Python en 2001. Timsort analiza primero la lista que está tratando de clasificar y luego elige un enfoque basado en el análisis de la lista.
Desde que se inventó el algoritmo, se ha utilizado como algoritmo de clasificación predeterminado en Python, Java, la Plataforma Android y en GNU Octave.
La notación O grande de Timsort es O (n log n). Para aprender sobre la notación Big O, lea esto.

El tiempo de clasificación de Timsort es el mismo que el de Mergesort, que es más rápido que la mayoría de los otros tipos que puede conocer. Timsort en realidad hace uso de Insertion sort y Mergesort, como verás pronto.
Peters diseñó Timsort para usar elementos ya ordenados que existen en la mayoría de los conjuntos de datos del mundo real. Llama a estos elementos ya ordenados «corridas naturales». Itera sobre los datos recopilando los elementos en corridas y fusionando simultáneamente esas corridas en una sola.
El array tiene menos de 64 elementos
Si el array que estamos intentando ordenar tiene menos de 64 elementos, Timsort ejecutará un ordenamiento por inserción.
Una clasificación por inserción es una clasificación simple que es más efectiva en listas pequeñas. Es bastante lento en las listas más grandes, pero muy rápido con las listas pequeñas. La idea de un tipo de inserción es la siguiente:
- Vea los elementos uno por uno
- Construya una lista ordenada insertando el elemento en la ubicación correcta
Aquí hay una tabla de seguimiento que muestra cómo ordenar por inserción ordenaría la lista

En este caso estamos insertando los elementos recién ordenados en un nuevo sub-array, que comienza al inicio del array.
Aquí hay un gif que muestra la ordenación de inserción:
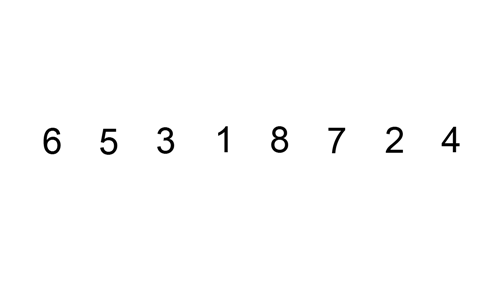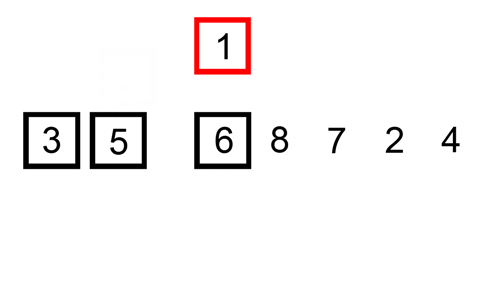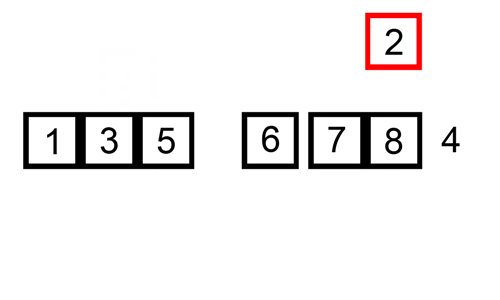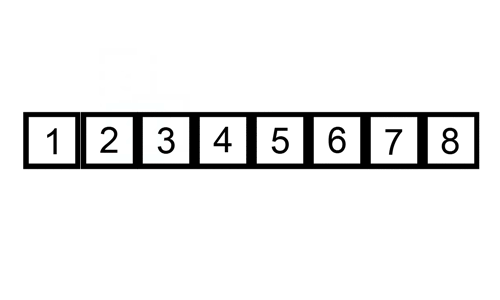
Más sobre corridas
Si la lista tiene más de 64 elementos, el algoritmo hará un primer paso por la lista buscando partes que estén estrictamente aumentando o disminuyendo. Si la parte está disminuyendo, invertirá esa parte.
Así que si la carrera está disminuyendo, se verá así (donde la carrera está en negrita):

Si no disminuye, se verá así:

El minrun es un tamaño que se determina en función del tamaño de la matriz. El algoritmo lo selecciona para que la mayoría de las ejecuciones en una matriz aleatoria tengan, o se conviertan en minrun, en longitud. Fusionar 2 matrices es más eficiente cuando el número de ejecuciones es igual o ligeramente inferior a una potencia de dos. Timsort elige minrun para intentar garantizar esta eficiencia, asegurándose de que minrun sea igual o inferior a una potencia de dos.
El algoritmo elige minrun del rango 32 al 64 inclusive. Elige minrun de tal manera que la longitud de la matriz original, cuando se divide por minrun, es igual o ligeramente inferior a una potencia de dos.
Si la duración de la carrera es menor que minrun, se calcula la duración de esa carrera alejada de minrun. Con este nuevo número, toma tantos elementos antes de la ejecución y realiza una clasificación de inserción para crear una nueva ejecución.
Así que si minrun es 63 y la duración de la carrera es 33, se hace 63-33 = 30. A continuación, se toman 30 elementos de delante del final de la ejecución, por lo que se trata de 30 elementos de la ejecución y, a continuación, se realiza una ordenación de inserción para crear una nueva ejecución.
Después de que esta parte se haya completado, ahora deberíamos tener un montón de ejecuciones ordenadas en una lista.
Fusión

Timsort ahora realiza mergesort para fusionar las ejecuciones. Sin embargo, Timsort se asegura de mantener la estabilidad y el equilibrio de fusión mientras se combina la clasificación.
Para mantener la estabilidad no debemos intercambiar 2 números de igual valor. Esto no solo mantiene sus posiciones originales en la lista, sino que permite que el algoritmo sea más rápido. En breve discutiremos el equilibrio de fusión.
A medida que se ejecuta Timsort finds, los agrega a una pila. Una pila simple se vería así:

Imagine una pila de placas. No puedes tomar platos de abajo, así que tienes que tomarlos de arriba. Lo mismo es cierto sobre una pila.
Timsort intenta equilibrar dos necesidades competidoras cuando se ejecuta mergesort. Por un lado, nos gustaría retrasar la fusión el mayor tiempo posible para explotar patrones que puedan surgir más adelante. Pero nos gustaría aún más hacer la fusión lo antes posible para explotar la ejecución que la ejecución que acaba de encontrar sigue siendo alta en la jerarquía de memoria. Tampoco podemos retrasar la fusión «demasiado tiempo» porque consume memoria para recordar las ejecuciones que aún no se han fusionado, y la pila tiene un tamaño fijo.
Para asegurarse de que tenemos este compromiso, Timsort realiza un seguimiento de los tres elementos más recientes de la pila y crea dos leyes que deben ser válidas para esos elementos:
1. A > B + C
2. B > C
Donde A, B y C son los tres elementos más recientes de la pila.
En palabras del propio Tim Peters:
Lo que resultó ser un buen compromiso mantiene dos invariantes en las entradas de la pila, donde A, B y C son las longitudes de las tres secciones a la derecha que aún no se han fusionado
Por lo general, la fusión de carreras adyacentes de diferentes longitudes en su lugar es difícil. Lo que lo hace aún más difícil es que tenemos que mantener la estabilidad. Para evitar esto, Timsort deja de lado la memoria temporal. Coloca la más pequeña (llamando a las dos carreras A y B) de las dos carreras en esa memoria temporal.
Galopando

Mientras Timsort está fusionando A y B, se da cuenta de que una carrera ha sido «ganadora» muchas veces seguidas. Si resultara que la carrera A consistía en números completamente más pequeños que la carrera B, entonces la carrera A terminaría en su lugar original. Fusionar las dos carreras implicaría mucho trabajo para no lograr nada.
La mayoría de las veces, los datos tendrán alguna estructura interna preexistente. Timsort asume que si muchos de los valores de la ejecución A son más bajos que los valores de la ejecución B, es probable que A siga teniendo valores más pequeños que B.
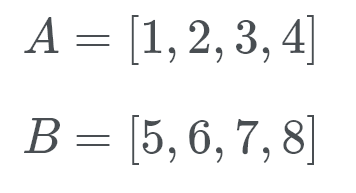
Timsort entrará en modo galopante. En lugar de comparar A y B entre sí, Timsort realiza una búsqueda binaria de la posición adecuada de b en a. De esta manera, Timsort puede mover una sección completa de A a su lugar. Luego, Timsort busca la ubicación adecuada de A en B. Timsort moverá una sección completa de la lata B a la vez y la colocará en su lugar.
Veamos esto en acción. Timsort comprueba B (que es 5) y usando una búsqueda binaria busca la ubicación correcta en A.
Bueno, B pertenece al final de la lista de A. Ahora Timsort comprueba A (que es 1) en la ubicación correcta de B. Así que estamos buscando ver dónde va el número 1. Este número va al principio de B. Ahora sabemos que B pertenece al final de A y A pertenece al principio de B.
Resulta que esta operación no vale la pena si la ubicación adecuada para B está muy cerca del comienzo de A (o viceversa). así que el modo galope sale rápidamente si no está dando sus frutos. Además, Timsort toma nota y hace que sea más difícil ingresar al modo galope más tarde al aumentar el número de victorias consecutivas de solo A o solo B necesarias para ingresar. Si el modo galope está dando sus frutos, Timsort facilita el reingreso.
En resumen, Timsort hace 2 cosas increíblemente bien:
- Gran rendimiento en matrices con estructura interna preexistente
- Ser capaz de mantener una clasificación estable
Anteriormente, para lograr una clasificación estable, tendría que comprimir los elementos de su lista con enteros y ordenarlos como una matriz de tuplas.
Código
Si no está interesado en el código, no dude en omitir esta parte. Hay más información debajo de esta sección.
El código fuente a continuación se basa en el trabajo mío y de Nanda Javarma. El código fuente no está completo, ni es similar al código fuente oficial ordenado() de Python. Esto es solo un Timsort aturdido que implementé para tener una idea general de Timsort. Si quieres ver el código fuente original de Timsort en todo su esplendor, échale un vistazo aquí. Timsort está implementado oficialmente en C, no en Python.
Timsort está construido directamente en Python, por lo que este código solo sirve como explicador. Para usar Timsort simplemente escriba:
list.sort()
O
sorted(list)
Si desea dominar cómo funciona Timsort y tener una idea de ello, le sugiero que intente implementarlo usted mismo.
Este artículo se basa en la introducción original de Tim Peters a Timsort, que se encuentra aquí.