Hitausmomentti-tyypilliset poikkileikkaukset i

hitausmomentti tai hitausmomentti pinta – alalle – joka tunnetaan myös nimellä Pinta-alan toinen momentti-I, on muodon ominaisuus, jota käytetään ennustamaan palkkien taipumista, taipumista ja stressiä.

hitausmomentti – Imperiaaliset yksiköt

• inches4

hitausmomentti – metriset yksiköt

• mm4
• cm4
• m4

muunnos yksiköiden välillä

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4, 16×105 mm4 = 41.6 cm4

esimerkki – Inertiamomentti

9240 cm4 voidaan muuntaa mm4: ksi kertomalla arvolla 104

(9240 cm4) 104 = 9.24 107 mm4

Pinta-alan hitausmomentti (Pinta-alan hitausmomentti tai Pinta-alan toinen momentti)

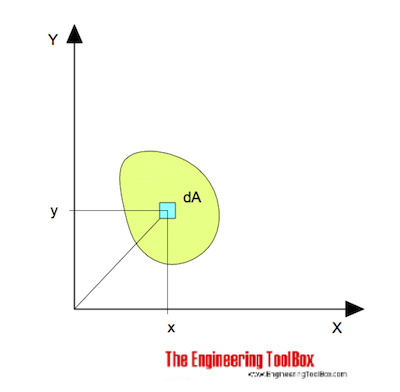
taivutettaessa x-akselin ympäri voidaan ilmaista muodossa

IX = ∫ Y2 dA (1)

IX = X-akseliin liittyvä hitausmomentti (m4, mm4, inches4)

y = kohtisuora etäisyys akselilta X elementtiin da (M, mm, tuumaa)

dA = alkuaineen pinta-ala (m2, mm2, inches2)

taivutuksen hitausmomentti y – akselin ympäri voidaan ilmoittaa

Iy = ∫ x2 dA (2)

missä

Iy = Y-akseliin liittyvä hitausmomentti (m4, mm4, inches4)

x = kohtisuora etäisyys akselista y alkuaineeseen dA (m, mm, tuumaa)

alueen hitausmomentti tyypillisille Poikkileikkauksille I

• hitausmomentti tyypillisten poikkileikkausten II osalta

kiinteän neliön poikkileikkaus

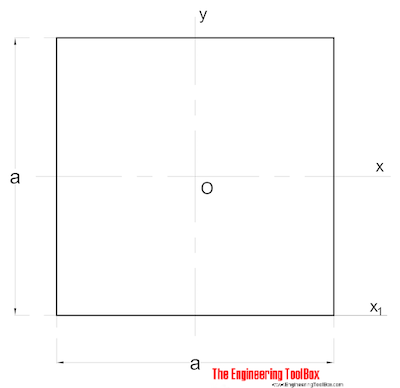
kiinteän neliön osan pinta-hitausmomentti voidaan laskea seuraavasti:

IX = a4 / 12 (2)

missä

a = sivu (mm, m, in..)

Iy = a4 / 12 (2b)

umpinainen suorakulmainen poikkileikkaus

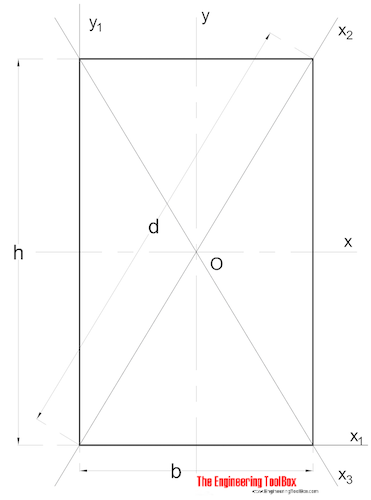
suorakulmaisen osan Inerian pinta-Alamomentti voidaan laskea seuraavasti:

Ix = B h3 / 12 (3)

jossa

b = leveys

h = korkeus

Iy = b3 h / 12 (3b)

kiinteän ympyrän muotoinen poikkileikkaus

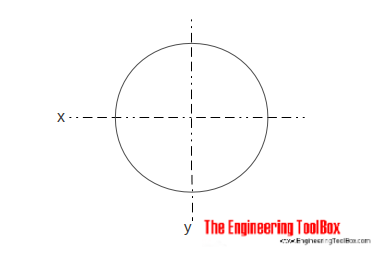
kiinteän lieriömäisen osan hitausmomentti voidaan laskea seuraavasti:

IX = π r4 / 4

= π d4 / 64 (4)

jossa

r = säde

d = halkaisija

Iy = π R4 / 4

= π D4 / 64 (4b)

ontto lieriömäinen poikkileikkaus

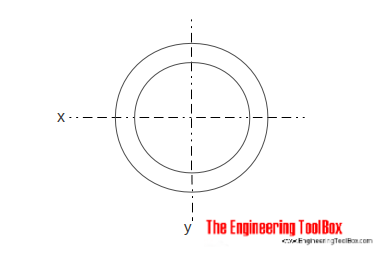
onton lieriömäisen osan hitausmomentti voidaan laskea seuraavasti:

IX = π (do4-di4) / 64 (5)

jossa

do = sylinterin ulkohalkaisija

di = sylinterin sisähalkaisija

Iy = π (do4-di4) / 64 (5b)

Neliöosuus – Lävistäjämomentit

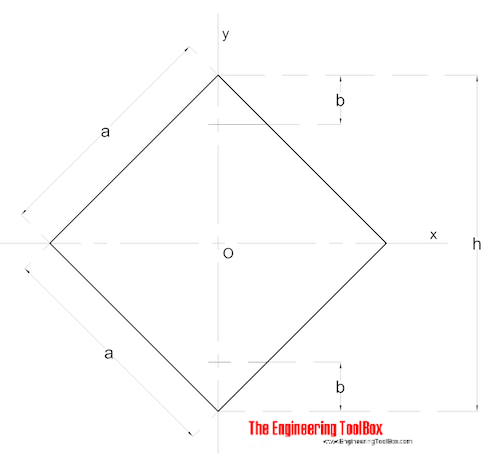
neliön osan Lävistäjämomentit voidaan laskea seuraavasti:

Ix = Iy = a4 / 12 (6)

suorakulmaiset poikkileikkauksen pinta-alamomentit millä tahansa painopisteen kautta kulkevalla suoralla

suorakaiteen muotoinen poikkileikkaus ja momentin pinta-ala painopisteen kautta kulkevalla suoralla voidaan laskea seuraavasti:

Ix = (b h / 12) (h2 cos2 A + B2 sin2 a) (7)

symmetrinen muoto

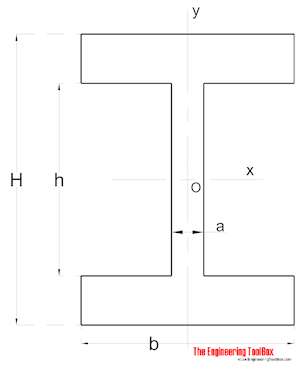
hitausmomentti symmetrisen muotoinen osa voidaan laskea seuraavasti:

Ix = (a h3 / 12) + (b / 12) (H3-h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

epäsymmetrinen muoto

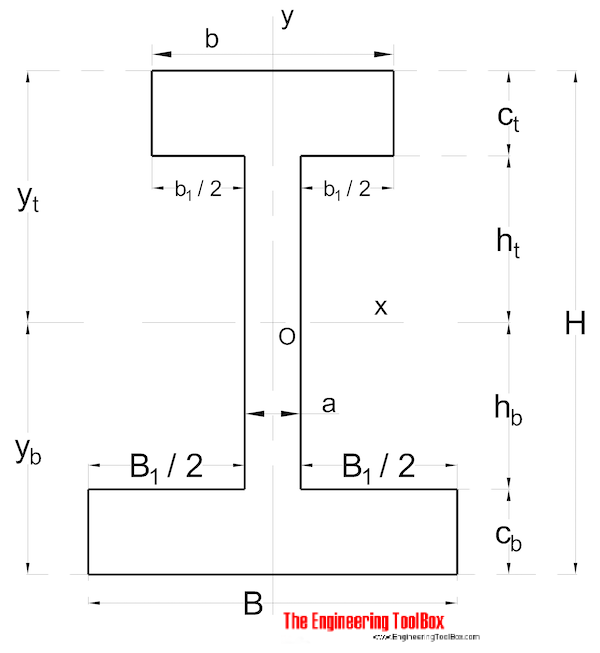
symmetrisen muotoisen osan hitausmomentti voidaan laskea seuraavasti:

Ix = (1 / 3) (B yb3 – B1 HB3 + b YT3-B1 HT3) (9)

• tyypillisten poikkileikkausten II hitausmomentti

hitausmomentti vs. Napamomentti vs. Hitausmomentti

• ”hitausmomentti” on muodon ominaisuus, jota käytetään ennustamaan taipumista, taipumista ja jännitystä palkeissa
• ”Napamomentti hitausmomentti” mittana säteen kyvystä vastustaa vääntöä – jota tarvitaan laskemaan momentille
• ”hitausmomentti” on kappaleen kiertokestävyyden mitta pyörimissuunnan muutoksille.

section Modulus

• ”Section Modulus” määritellään seuraavasti: W = I / y, jossa I on hitausmomentti ja y on etäisyys neutraalista akselista johonkin kuituun