Si notre objectif est de trouver la généralisation relativiste de l’équation de Poisson pour le champ gravitationnel:
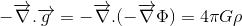
où Φ se réfère au potentiel gravitationnel et ρ à la densité de masse, nous sommes à mi-chemin.
En effet, nous avons déjà vu dans notre précédent article Le tenseur énergie-moment que la généralisation de la densité de masse (terme de droite de l’équation) correspond à l’énergie-moment Tµv.
Il semble donc raisonnable de supposer que notre équation devrait prendre la forme de:
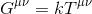
où k représente un scalaire et Gµv, appelé tenseur d’Einstein représente un tenseur de rang 2 décrivant la courbure de l’espace-temps.
À notre connaissance, le Gµv doit obéir aux contraintes suivantes:
– il devrait s’annuler dans l’espace-temps plat
– il devrait décrire la courbure de l’espace-temps et être linéaire par rapport au tenseur de Riemann
– il devrait être symétrique et de rang 2 (comme Tµv)
– il devrait avoir une divergence nulle (comme Tµv)
– et enfin, en newtonien aux limites, elle devrait se réduire à 4nGp
Première tentative avec le tenseur de Ricci comme solution
Nous rappelons de notre article L’équation géodésique dans la Limite newtonienne que le potentiel gravitationnel Φ est lié à la composante 00 de la métrique via h00 =(g00-1)/c2
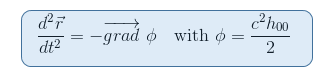
Il semble alors naturel de rechercher un tenseur qui fait intervenir les dérivées secondes de la métrique, ce qui est le cas pour le tenseur de Riemann. De plus, le tenseur de Riemann est le seul candidat que nous connaissons à ce jour pour pouvoir décrire la courbure de l’espace-temps (cf deuxième contrainte ci-dessus).
Comme nous devons trouver un tenseur de rang 2, et si nous supposons que nous devons trouver une solution uniquement en termes de tenseur de Riemann, il semble naturel de considérer d’abord la forme contractée du tenseur de Riemann, connu sous le nom de tenseur de Ricci.
Pour voir cela, rappelons l’expression du tenseur de Riemann de l’article Le tenseur de courbure de Riemann partie II: dérivation de la déviation géodésique
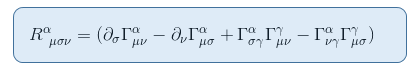
Dans la limite d’un champ gravitationnel statique et faible, un seul terme contribue à R00:
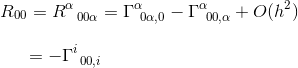
Dans le même article, nous avons calculé ce symbole de Christoffel et constaté que
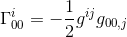
avec l’approximation de gij = nij et goo, j = hoo, j (reportez-vous à l’article), nous obtenons:
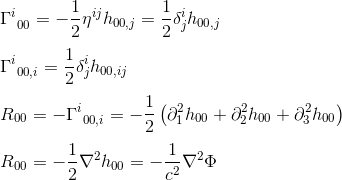
L’identification de R00 avec ΔΦ (opérateur laplacien) suggère que l’équation de champ en relativité générale devrait assimiler Rab à un multiple constant de Tab.
En 1915, en utilisant cette équation, Einstein a même pu résoudre le problème de longue date de la précession du périhélie de Mercure, ce qui a fait écrire en novembre de la même année que: « Pendant quelques jours, j’étais hors de moi avec une excitation joyeuse. »
Finalement, Einstein a dû rejeter cette première tentative, du fait qu’en général la divergence de Rab ne s’annule PAS.
Deuxième tentative
Il y a un tenseur étroitement lié au scalaire de Ricci qui peut être placé du côté gauche sans contradiction. Cela donne le tenseur d’Einstein défini comme suit:
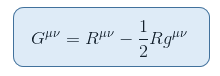
où R = Raa est le scalaire de Ricci ou la courbure scalaire.
Cette forme de Gab est symétrique et de rang 2 et décrit évidemment la courbure de l’espace-temps. Il ne reste donc plus qu’à montrer que la dérivée totale est nulle
Pour ce faire, nous commençons par l’identité Bianchi
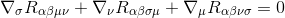
En multipliant par gγσgαμgβν (les dérivées métriques sont nulles, elles agissent donc comme des constantes et peuvent être prises à l’intérieur des dérivées), cela donne à:
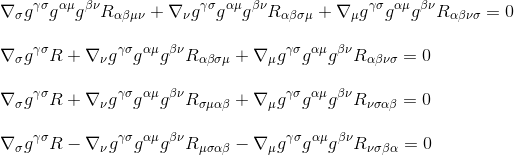
En utilisant la définition du tenseur de Ricci Rµv = gμβgνσRβσ (étape 3) et en renommant les indices (étape 4), on obtient
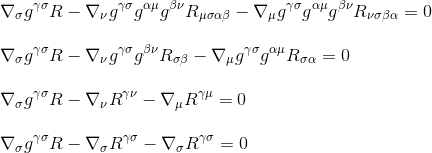
En factorisant la dérivée, on obtient finalement
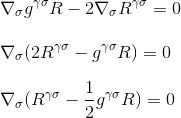
c’est exactement ce que nous voulions démontrer: la divergence du tenseur d’Einstein est nulle, et nous avons trouvé le bon candidat pour le côté gauche de notre équation courbure / masse-énergie.