ha célunk Poisson egyenletének relativisztikus általánosítása a gravitációs mezőre:
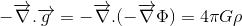
ahol a Gravitációspotenciálra, a tömegsűrűségre pedig a gravitációspotenciálra utal, félúton vagyunk.
valóban, már láttuk az előző cikkünkben az energia-momentum tenzor, hogy a tömegsűrűség általánosítása (az egyenlet jobb oldali kifejezése) megfelel a T energia-Momentumnak.
ésszerűnek tűnik tehát azt feltételezni, hogy egyenletünknek a következő formát kell öltenie:
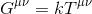
ahol k egy skalárt jelent, g pedig a G-t, az Einstein-tenzor a téridő görbületét leíró rank-2 tenzort képviseli .
amennyire tudjuk, a G-nak be kell tartania a következő korlátozásokat:
– sík téridőben semmissé kell tennie
– le kell írnia a téridő görbületét, és lineárisnak kell lennie a Riemann – tenzorhoz képest
– szimmetrikusnak kell lennie, és 2 – es rangúnak kell lennie (mint T++)
-null divergenciával kell rendelkeznie (mint T++)
-és végül, a newtoni határértékek, 4ngp-re kell csökkentenie
első kísérlet Ricci tenzorral mint megoldás
cikkünkből emlékeztetünk a newtoni határ geodéziai egyenletére, hogy a gravitációs potenciál a metrika 00-komponenséhez kapcsolódik H00=(G00-1)/C2
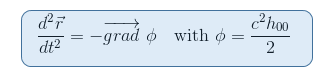
akkor természetesnek tűnik olyan tenzort keresni, amely magában foglalja a metrika második deriváltjait, ami a Riemann-tenzor esetében is így van. Továbbá a Riemann-tenzor az egyetlen jelölt, akit eddig ismerünk, hogy képes legyen leírni a téridő görbületét(vö.
mivel meg kell találnunk A rank-2 tenzort, és ha feltételezzük, hogy kizárólag a Riemann-tenzor szempontjából kell megoldást találnunk, természetesnek tűnik először a Riemann-tenzor összehúzott formáját, amelyet Ricci-tenzornak nevezünk.
ennek megtekintéséhez idézzük fel a Riemann-tenzor kifejezését Tha cikk a Riemann-görbületi tenzor II. rész: levezetés a geodéziai eltérésből
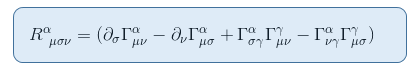
a statikus és gyenge gravitációs mező határában csak egy kifejezés járul hozzá az R00-hoz:
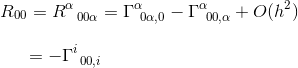
ugyanebben a cikkben kiszámítottuk ezt a Christoffel szimbólumot, és megállapítottuk, hogy
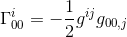
a gij = nij és a goo,j = hoo,j (lásd a cikket) közelítésével megkapjuk:
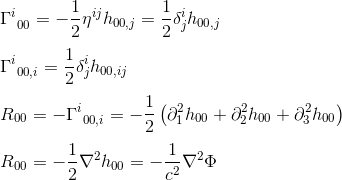
az R00 azonosítása a (Laplacian operátor) azt sugallja, hogy az Általános relativitáselméletben a mezőegyenletnek egyenlőnek kell lennie rab a TAB állandó többszörösével.
1915-ben ezt az egyenletet használva Einstein még a Merkúr perihelion precessziójának régóta fennálló problémáját is képes volt megoldani, aminek következtében az év novemberében ezt írta: “néhány napig magam mellett voltam örömteli izgalommal.”
végül Einsteinnek el kellett utasítania ezt az első kísérletet, mivel a Rab általános eltérése nem semmisíti meg.
második kísérlet
van tenzor szorosan kapcsolódik a Ricci skalár wihch tudunk a bal oldalon ellentmondás nélkül. Ez az Einstein-tenzort a következőképpen határozza meg:
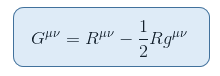
ahol R = Raa a Ricci skalár vagy skalár görbülete.
a Gab ezen formája szimmetrikus és 2-es rangú, és nyilvánvalóan leírja a téridő görbületét. Tehát csak azt kell megmutatni, hogy a teljes derivált nulla
ehhez a Bianchi identitással kezdjük
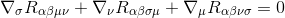
megszorozzuk g-vel (a metrikák deriváltjai nullák, tehát állandóként működnek, és a deriváltakon belül vehetők fel), ez a következőt eredményezi::
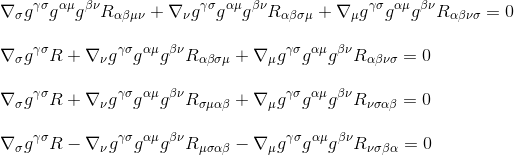
a Ricci tenzor definícióját használva R (3. lépés) és az indexek átnevezésével (4. lépés) megkapjuk
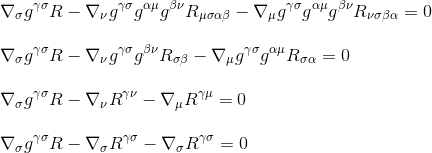
a derivált faktorizálásával végül megkapjuk
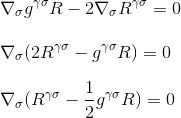
pontosan ezt akartuk bizonyítani: az Einstein-tenzor divergenciája nulla, és megtaláltuk a megfelelő jelöltet a görbület/tömeg-energia egyenlet bal oldalára.