interkvartilis tartományok & kiugró értékek

• Purplemath
• MathHelp.com
• keresse meg a következő adatkészlet kiugró értékeit, ha vannak ilyenek:
• keresse meg a következő adatkészlet kiugró értékeit és szélső értékeit, ha vannak ilyenek, és rajzolja meg a box-and-whisker ábrát. Jelöljön meg minden kiugró értéket csillaggal, az extrém értékeket pedig nyitott ponttal.

Purplemath

az “interkvartilis tartomány”, rövidítve “IQR”, csak a doboz szélessége a box-and-whisker diagramban. Vagyis IQR = Q3-Q1 . Az IQR használható az értékek eloszlásának mérésére.

a statisztikák azt feltételezik, hogy az értékek valamilyen központi érték köré csoportosulnak. Az IQR megmondja, hogy a “középső” értékek mennyire vannak elosztva; arra is használható, hogy megmondja, ha a többi érték “túl messze van” a központi értéktől. Ezeket a” túl messze “pontokat” kiugró értékeknek “nevezzük, mert” kívül esnek ” azon a tartományon, amelyben elvárjuk őket.

az IQR a doboz hossza a box-and-whisker telken. Kiugró érték minden olyan érték, amely a doboz hosszának több mint másfélszerese a doboz mindkét végétől.

A tartalom alább folytatódik

MathHelp.com

ez azt jelenti, hogy ha egy adatpont Q alatt van1 – 1,5 kb IQR vagy Q Felett3 + 1,5 kb IQR, úgy tekintik, hogy túl messze van a központi értékektől ahhoz, hogy ésszerű legyen. Lehet, hogy nekimentél a mérlegnek, amikor ezt az egy mérést végezted, vagy talán a laborpartnered egy idióta, és soha nem kellett volna hagynod, hogy megérintse a berendezéseket. Ki tudja? De bármi is legyen az okuk, a kiugró pontok azok a pontok, amelyek úgy tűnik, hogy nem “illenek”.

miután kényelmesen megtalálta az IQR-t, folytathatja a kiugró értékek megtalálását, ha vannak ilyenek.

• keresse meg a következő adatkészlet kiugró értékeit, ha vannak ilyenek:

a Q1 – 1,5 (IQR) és a Q3 + 1,5 (IQR) (IQR) értékek azok a “kerítések”, amelyek az “ésszerű” értékeket jelölik ki a kiugró értékekből. A kívülállók a kerítésen kívül fekszenek.

ha a hozzárendelés nem csak a kiugró értékeket, hanem a “szélsőséges értékeket” is figyelembe veszi, akkor a Q1 – 1 értékei.5 6-3 + 1,5 0x és Q3 + 1,5 xx a “belső” kerítések, míg a Q1 – 3 3 XX és Q3 + 3 xx a “külső” kerítések.

a kiugró értékek (csillagokkal vagy nyitott pontokkal jelölve) a belső és a külső kerítések között vannak, a szélső értékek pedig (bármelyik szimbólummal jelölve, amelyet nem használt a kiugró értékekhez) a külső kerítéseken kívül vannak.

Apropó, a könyv hivatkozhat az értéke “1,5 6g IQR”, hogy a “lépés”. Ezután a kiugró számok azok a számok, amelyek a csuklópántoktól egy-két lépés között vannak, a szélsőséges érték pedig azok a számok, amelyek több mint két lépésre vannak a csuklópántoktól.

az előző példát ismét megvizsgálva a külső kerítések 14,4 – 3 0,5 = 12,9 és 14,9 + 3 0,5 = 16,4. Mivel az 16.4 közvetlenül a felső külső kerítésen van, ez csak egy kiugró értéknek tekinthető, nem pedig szélsőséges értéknek. De a 10,2 teljesen az alsó külső kerítés alatt van, tehát a 10,2 extrém érték lenne.

a grafikus számológép lehet, hogy nem jelzi, hogy a box-and-whisker plot tartalmaz kiugró értékeket. Például a fenti probléma magában foglalja a 10.2, 15.9 és 16.4 pontokat, mint kiugró értékeket. A grafikus számológépem egyik beállítása megadja az egyszerű box-and-whisker diagramot, amely csak az öt számú összefoglalót használja, így a legtávolabbi kiugró értékek jelennek meg a bajuszok végpontjaként:

egy másik számológép-beállítás megadja a box-and-whisker-ábrát a kiugró értékek külön megjelölésével (ebben az esetben egy nyitott pont szimulációjával), és a bajusz csak a legmagasabb és a legalacsonyabb értékig megy, amelyek nem kiugró értékek:

a számológépem nem tesz különbséget a kiugró értékek és a szélsőséges értékek között. Talán a tiéd sem. Ellenőrizze a használati útmutatót most, a következő teszt előtt.

ha a grafikus számológépet használja, hogy segítsen ezeken a telkeken, győződjön meg róla, hogy tudja, melyik beállítást használja, és mit jelent az eredmény, vagy a számológép tökéletesen helyes, de “rossz” választ adhat.

• keresse meg a következő adatkészlet kiugró értékeit és szélső értékeit, ha vannak ilyenek, és rajzolja meg a box-and-whisker ábrát. Jelöljön meg minden kiugró értéket csillaggal, az extrém értékeket pedig nyitott ponttal.

hirdetés

a kiugró értékek és a szélsőséges értékek megtalálásához először meg kell találnom az IQR-t. Mivel hét érték van a listában, a medián a negyedik érték, tehát:

Q2 = 25

a lista első fele:

21, 23, 24

…tehát Q1 = 23; a második fele:

29, 33, 49

…tehát Q3 = 33. Ezután az IQR-t megadja:

IQR = 33 – 23 = 10

a kiugró értékek az alábbi értékek lesznek:

23 – 1.5×10 = 23 – 15 = 8

…vagy a fenti:

33 + 1.5×10 = 33 + 15 = 48

a szélsőséges értékek az alábbiak lesznek:

23 – 3×10 = 23 – 30 = -7

…vagy a fenti:

33 + 3×10 = 33 + 30 = 63

tehát van egy kiugró a 49 de nincsenek szélsőséges értékek. Nem lesz felső bajuszom a cselekményemen, mert a Q3 is a legmagasabb, nem kiugró. Tehát a telek így néz ki:

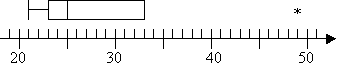
meg kell jegyezni, hogy a fent vázolt módszerek, kifejezések és szabályok azok, amelyeket tanítottam, és amelyeket a leggyakrabban láttam tanítani. A tanfolyamnak azonban eltérő speciális szabályai lehetnek, vagy a számológép kissé eltérően végezheti el a számításokat. Lehet, hogy kissé rugalmasnak kell lennie a tantervére vonatkozó válaszok megtalálásában.