Area Momento di inerzia-Sezioni trasversali tipiche I

Area Momento di inerzia o Momento di inerzia per un’area – noto anche come Secondo momento di Area – I, è una proprietà della forma che viene utilizzata per prevedere la deflessione, la flessione e lo stress nelle travi.

Momento di Inerzia – Imperiale

• inches4

Momento di Inerzia – unità Metriche

• mm4
• cm4
• m4

Conversione tra Unità di

• 1 cm4 = 10-8 m4 = 104 mm4
• 1 in4 = 4.16×105 mm4 = 41.6 cm4

Esempio – Conversione tra unità di momento d’inerzia

9240 cm4 può essere convertito in mm4 moltiplicando con 104

(9240 cm4) 104 = 9.24 107 mm4

Momento di Inerzia (Momento di Inerzia di un’Area o di un Secondo Momento di Area)

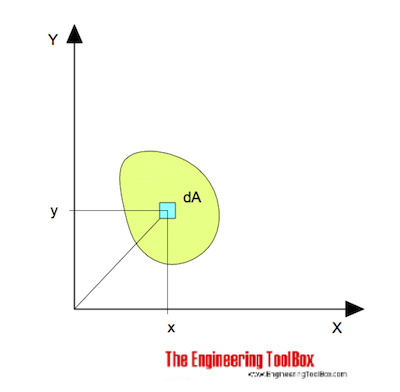
per flettente intorno all’asse x può essere espresso come

Ix = ∫ y2 dA (1)

dove

Ix = Momento di Inerzia relativi all’asse x (m4, mm4, inches4)

y = distanza perpendicolare all’asse x per l’elemento dA (m, mm, pollici)

dA = un elementale superficie (m2, mm2, inches2)

Il Momento di Inerzia a flessione intorno all’asse y può essere espresso come

Iy = ∫ x2 dA (2)

dove

Iy = Momento di Inerzia relativi all’asse y (m4, mm4, inches4)

x = distanza perpendicolare all’asse y l’elemento dA (m, mm, pollici)

Momento di Inerzia per i tipici Sezioni I

• Momento di Inerzia per i tipici Sezioni II

Massello a Sezione Quadrata

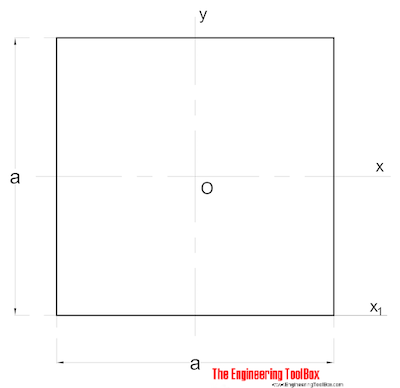
Il Momento di Inerzia di un solido a sezione quadrata può essere calcolato come

Ix = a4 / 12 (2)

dove

a = lato (mm, m, in..)

Iy = a4 / 12 (2b)

Massello a Sezione Rettangolare

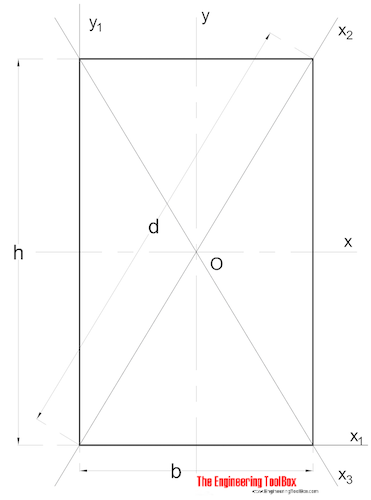
I Momento di Ineria per una sezione rettangolare può essere calcolato come

Ix = b h3 / 12 (3)

dove

b = larghezza

h = altezza

Iy = b3 h / 12 (3b)

Massello a Sezione Circolare

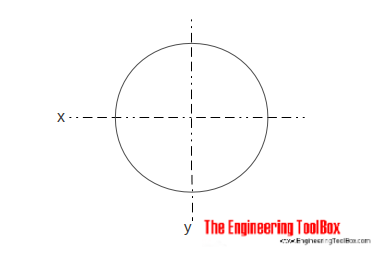
Il Momento di Inerzia di un solido cilindrico di sezione può essere calcolato come

Ix = π r4 / 4

= π d4 / 64 (4)

dove

r = raggio

d = diametro

Iy = π r4 / 4

= π d4 / 64 (4b)

Cilindrico Cavo con Sezione a Croce

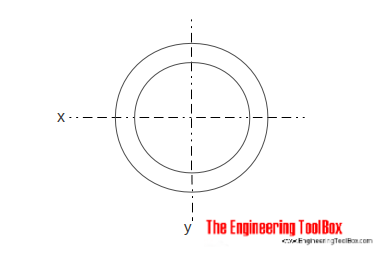
Il Momento di Inerzia per un cavo di sezione cilindrica, può essere calcolato come

Ix = π (do4 – di4) / 64 (5)

dove

do = cilindro diametro esterno

di = diametro interno del cilindro

Iy = π (do4 – di4) / 64 (5b)

Sezione Quadrata – Diagonale Momenti

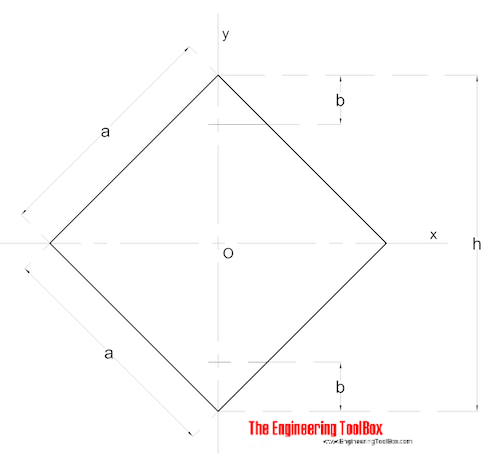
Area diagonale Momenti di Inerzia di una sezione quadrata può essere calcolato come

Ix = Iy = a4 / 12 (6)

Sezione rettangolare – Area Momenti su qualsiasi linea attraverso il Centro di Gravità

sezione Rettangolare e l’Area del Momento sulla linea attraverso il Centro di Gravità può essere calcolato come

Ix = (b h / 12) (h2 cos2 a + b2 sin2 un) (7)

Forma Simmetrica

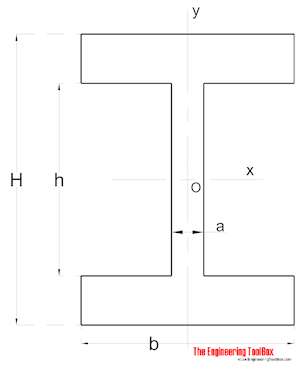
Momento di Inerzia per un simmetrica a forma di sezione può essere calcolato come

Ix = (a h3 / 12) + (b / 12) (H3 – h3) (8)

Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)

Nonsymmetrical Forma

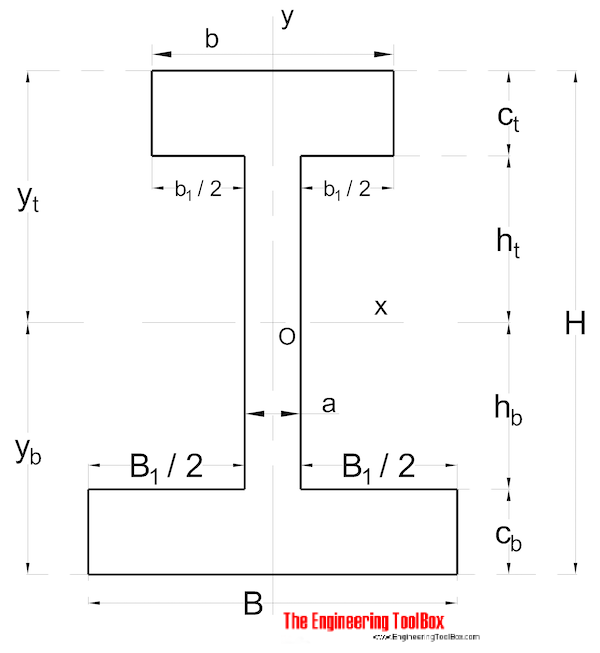
Momento di Inerzia per non simmetrica a forma di sezione può essere calcolato come

Ix = (1 / 3) (B yb3 – B1 hb3 + b yt3 – b1 ht3) (9)

• Momento di Inerzia per i tipici Sezioni II

Momento di Inerzia vs Momento di Inerzia Polare vs Momento di Inerzia

• “Momento di Inerzia” è una struttura di forma che viene utilizzato per prevedere flessione, piegatura e di sollecitazione nelle travi
• “Momento di Inerzia Polare” come misura di un fascio capacità di resistere alla torsione, che è necessario per calcolare il tocco di una trave sottoposta a coppia
• “Momento di Inerzia” è una misura di un oggetto, la resistenza al cambiamento nella direzione di rotazione.

Modulo di sezione

• il” Modulo di sezione ” è definito come W = I / y, dove I è il momento di inerzia dell’area e y è la distanza dall’asse neutro a qualsiasi fibra data