Si prega di fornire numeri separati da virgola per calcolare.
Statistiche correlate Calculator / Deviazione standard Calculator / Sample Size Calculator
Mean
La parola mean, che è un omonimo per più altre parole in lingua inglese, è altrettanto ambigua anche nel campo della matematica. A seconda del contesto, sia matematico che statistico, ciò che si intende per “media” cambia. Nella sua definizione matematica più semplice per quanto riguarda i set di dati, la media utilizzata è la media aritmetica, indicata anche come aspettativa matematica, o media. In questa forma, la media si riferisce a un valore intermedio tra un insieme discreto di numeri, vale a dire la somma di tutti i valori nel set di dati, diviso per il numero totale di valori. L’equazione per il calcolo di una media aritmetica è praticamente identica a quella per il calcolo dei concetti statistici di popolazione e media campionaria, con leggere variazioni nelle variabili utilizzate:
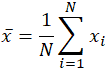
La media è spesso indicata come x, pronunciata “x bar”, e anche in altri usi quando la variabile non è x, la notazione della barra è un indicatore comune di una qualche forma di media. Nel caso specifico della media della popolazione, piuttosto che usare la variabile x, viene utilizzato il simbolo greco mu, o μ. Allo stesso modo, o piuttosto confusamente, la media del campione nelle statistiche è spesso indicata con una X maiuscola. Dato il set di dati 10, 2, 38, 23, 38, 23, 21, applicando la somma sopra i rendimenti:
|
10 + 2 + 38 + 23 + 38 + 23 + 21
|
= | = 22.143 |
Come accennato in precedenza, questo è uno dei più semplici definizioni di media, e alcuni altri sono la media aritmetica (che è diverso in alcuni valori nel set di dati di contribuire più valore di altri), e la media geometrica. Una corretta comprensione di determinate situazioni e contesti può spesso fornire a una persona gli strumenti necessari per determinare quale metodo statisticamente rilevante utilizzare. In generale, media, mediana, modalità e intervallo dovrebbero idealmente essere calcolati e analizzati per un determinato campione o set di dati poiché chiariscono diversi aspetti dei dati forniti e, se considerati da soli, possono portare a false dichiarazioni dei dati, come sarà dimostrato nelle sezioni seguenti.
Mediana
Il concetto statistico della mediana è un valore che divide un campione di dati, una popolazione o una distribuzione di probabilità in due metà. Trovare la mediana implica essenzialmente trovare il valore in un campione di dati che ha una posizione fisica tra il resto dei numeri. Si noti che quando si calcola la mediana di un elenco finito di numeri, l’ordine dei campioni di dati è importante. Convenzionalmente, i valori sono elencati in ordine crescente, ma non esiste una vera ragione per cui elencare i valori in ordine decrescente fornirebbe risultati diversi. Nel caso in cui il numero totale di valori in un campione di dati sia dispari, la mediana è semplicemente il numero al centro dell’elenco di tutti i valori. Quando il campione di dati contiene un numero pari di valori, la mediana è la media dei due valori medi. Mentre questo può essere fonte di confusione, ricorda semplicemente che anche se la mediana a volte comporta il calcolo di una media, quando si verifica questo caso, coinvolgerà solo i due valori medi, mentre una media coinvolge tutti i valori nel campione di dati. Nei casi dispari in cui ci sono solo due campioni di dati o c’è un numero pari di campioni in cui tutti i valori sono uguali, la media e la mediana saranno uguali. Dato lo stesso set di dati di prima, la mediana verrebbe acquisita nel modo seguente:
2,10,21,23,23,38,38
Dopo aver elencato i dati in ordine crescente e aver determinato che esiste un numero dispari di valori, è chiaro che 23 è la mediana dato questo caso. Se ci fosse un altro valore aggiunto al set di dati:
2,10,21,23,23,38,38,1027892
Poiché ci sono un numero pari di valori, la mediana sarà la media dei due numeri centrali, in questo caso 23 e 23, la cui media è 23. Si noti che in questo particolare set di dati, l’aggiunta di un outlier (un valore ben al di fuori dell’intervallo di valori previsto), il valore 1,027,892, non ha alcun effetto reale sul set di dati. Se tuttavia viene calcolata la media per questo set di dati, il risultato è 128,505.875. Questo valore non è chiaramente una buona rappresentazione degli altri sette valori nel set di dati che sono molto più piccoli e più vicini in valore rispetto alla media e all’outlier. Questo è il principale vantaggio dell’utilizzo della mediana nella descrizione dei dati statistici rispetto alla media. Mentre entrambi, così come altri valori statistici, dovrebbero essere calcolati quando si descrivono i dati, se solo uno può essere utilizzato, la mediana può fornire una stima migliore di un valore tipico in un dato set di dati quando ci sono variazioni estremamente grandi tra i valori.
Modalità
Nelle statistiche, la modalità è il valore in un set di dati con il maggior numero di ricorrenze. È possibile che un set di dati sia multimodale, il che significa che ha più di una modalità. Ad esempio:
2,10,21,23,23,38,38
Sia 23 che 38 appaiono due volte ciascuno, rendendoli entrambi una modalità per il set di dati sopra.
Analogamente alla media e alla mediana, la modalità viene utilizzata come modo per esprimere informazioni su variabili casuali e popolazioni. A differenza di media e mediana, tuttavia, la modalità è un concetto che può essere applicato a valori non numerici come la marca di tortilla chips più comunemente acquistati da un negozio di alimentari. Ad esempio, quando si confrontano i marchi Tostitos, Mission e XOCHiTL, se si scopre che nella vendita di tortilla chips, XOCHiTL è la modalità e vende in un rapporto di 3:2:1 rispetto a Tostitos e Mission brand tortilla chips rispettivamente, il rapporto potrebbe essere utilizzato per determinare il numero di sacchetti di ogni marca a magazzino. Nel caso in cui 24 sacchetti di tortilla chips vendano durante un dato periodo, il negozio immagazzinerebbe 12 sacchetti di chip XOCHiTL, 8 di Tostitos e 4 di Mission se si utilizza la modalità. Se tuttavia il negozio semplicemente utilizzato una media e venduto 8 sacchetti di ciascuno, potrebbe potenzialmente perdere 4 vendite se un cliente desiderato solo chip XOCHiTL e non qualsiasi altra marca. Come è evidente da questo esempio, è importante prendere in considerazione tutte le maniere dei valori statistici quando si tenta di trarre conclusioni su qualsiasi campione di dati.
Intervallo
L’intervallo di un set di dati nelle statistiche è la differenza tra i valori più grandi e quelli più piccoli. Mentre la gamma ha significati diversi all’interno di diverse aree della statistica e della matematica, questa è la sua definizione più basilare ed è ciò che viene utilizzato dalla calcolatrice fornita. Usando lo stesso esempio:
2,10,21,23,23,38,38
38 – 2 = 36
L’intervallo in questo esempio è 36. Analogamente alla media, l’intervallo può essere significativamente influenzato da valori estremamente grandi o piccoli. Usando lo stesso esempio di prima: