導関数を使用して最大値と最小値を求める

例：ボールが空中に投げられる。 いつでもその高さtは次のように与えられます。

h=3+14t−5t2

その最大の高さは何ですか？

導関数を使用して、その関数の傾きを見つけることができます:

h=0 + 14 − 5(2t)
=14−10t

（その導関数をどのように見つけたかについては、この例の下を参照してください。)

傾きがゼロのときを見つける：

傾きはt=1.4秒でゼロ

そのときの高さは

だから：

最大の高さは12.8mです（t=1.4sで)

デリバティブに関する簡単な復習

デリバティブは基本的に関数の傾きを見つけます。

前の例では、

h=3+14t−5t2

となり、この導関数を考え出しました:

h=0 + 14 − 5(2t)
=14−10t

これは、いつでも関数の傾きを示しますt

私たちはこれらの派生規則を使用しました:

• 定数値（3など）の傾きは0
• 2xのような線の傾きは2なので、14tの傾きは14
• t2のような正方形関数の傾きは2tなので、5t2の傾きは5(2t)
• : 0 + 14 − 5（2トン)

これは二次微分検定と呼ばれます

二次微分検定

関数の傾きがxでゼロで、xでの二次導関数が次のようになるとき、次のようになります。:

• 0より小さい場合、0より大きいローカル最大値
• 0に等しいローカル最小値
• テストは失敗します（ただし、他の方法がある可能性があります)

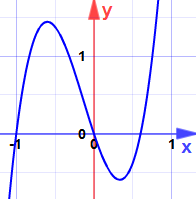
例：のための最大値と最小値を求める：y=5×3+2×2−3x

導関数（傾き）は次のとおりです:

y=15×2+4x− 3

これはゼロを持つ二次である:

• ×= -3/5
• x= +1/3

彼らは最大値または最小値である可能性がありますか？ （まだグラフを見てはいけません！2830>

二次導関数は、xにおいてy”=30x+4

です。= -3/5:

です= +1/3:

です（グラフを見ることができます。)

高い点は最大値（複数形の最大値）と呼ばれます。

低い点は最小値（複数形の最小値）と呼ばれます。

最大値または最小値の一般的な単語は、極値（複数形極値）です。

他の場所に高い（または低い）点があるかもしれないが、近くにない場合、局所的な最大値（または最小値）と言います。

例：最大値と最小値を求める：

y=x3−6×2+12x−5

導関数は次のとおりです:

y=3×2−12x+ 12

x=2

でゼロが1つだけの二次式はどれですか？2次導関数は、x=2でy”=6x−12

です。

そしてここに理由があります:

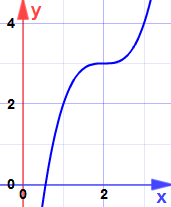
それは鞍点です。.. 傾きはゼロになりますが、最大値でも最小値でもありません。

例：関数f（x）=|x|（絶対値）はどうですか？

|x|次のようになります:

x=0では、それは非常に先のとがった変化を持っています！

実際、そこでは微分可能ではありません（微分可能なページに示されているように）。

したがって、絶対値関数にこのメソッドを使用することはできません。